请注意这是由另外的假设体系导出交换律，　与此同时，　算术公理体系也可以参考这里 http://en.wikipedia.org/

来源: littlecat8 于 2014-07-11 10:41:39 [] [博客] [旧帖] [给我悄悄话] 阅读数 : (15405 bytes)
回答: Really??? 由 26484915 于 2014-07-11 10:18:08

There are many different, but equivalent, axiomatizations of Peano arithmetic. While some axiomatizations, such as the one just described, use a signature that only has symbols for 0 and the successor, addition, and multiplications operations, other axiomatizations use the language of ordered semirings, including an additional order relation symbol. One such axiomatization begins with the following axioms that describe a discrete ordered semiring.[8]

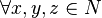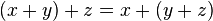  1. \forall x, y, z \in N. (x + y) + z = x + (y + z), i.e., addition is associative.
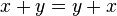  2. \forall x, y \in N. x + y = y + x, i.e., addition is commutative.
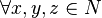  3. \forall x, y, z \in N. (x \cdot y) \cdot z = x \cdot (y \cdot z), i.e., multiplication is associative.
  4. \forall x, y \in N. x \cdot y = y \cdot x, i.e., multiplication is commutative.
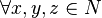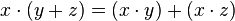  5. \forall x, y, z \in N. x \cdot (y + z) = (x \cdot y) + (x \cdot z), i.e., the distributive law.
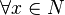  6. \forall x \in N. x + 0 = x \and x \cdot 0 = 0, i.e., zero is the identity element for addition.
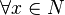  7. \forall x \in N. x \cdot 1 = x, i.e., one is the identity element for multiplication.
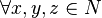  8. \forall x, y, z \in N. x < y \and y < z \Rightarrow x < z, i.e., the '<' operator is transitive.
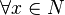  9. \forall x \in N. \neg (x < x), i.e., the '<' operator is irreflexive.
  10. \forall x, y \in N. x < y \or x = y \or y < x.
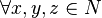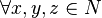  11. \forall x, y, z \in N. x < y \Rightarrow x + z < y + z.
  12. \forall x, y, z \in N. 0 < z \and x < y \Rightarrow x \cdot z < y \cdot z.
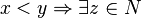  13. \forall x, y \in N. x < y \Rightarrow \exists z \in N. x + z = y.
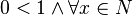  14. 0 < 1 \and \forall x \in N. x > 0 \Rightarrow x \geq 1.
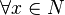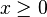  15. \forall x \in N. x \geq 0.

The theory defined by these axioms is known as PA–; PA is obtained by adding the first-order induction schema.

所有跟帖： 

• 数学专家，鉴定完毕~~ -随意- ♀ 给 随意 发送悄悄话 随意 的博客首页 (0 bytes) () 07/11/2014 postreply 10:44:24

• 专家谈不上，只是懂一点皮毛而已。。。 -littlecat8- ♂ 给 littlecat8 发送悄悄话 littlecat8 的博客首页 (0 bytes) () 07/11/2014 postreply 10:49:37

• 你好像是鉴定专家啊，你上一次那个鉴定我觉得很有水平啊，哈哈 -医者意也- ♂ 给 医者意也 发送悄悄话 医者意也 的博客首页 (0 bytes) () 07/11/2014 postreply 10:52:55

• thx for noticing my finding on the couple relationship -随意- ♀ 给 随意 发送悄悄话 随意 的博客首页 (61 bytes) () 07/11/2014 postreply 11:43:34

• Can you challenge those? -26484915- ♂ 给 26484915 发送悄悄话 26484915 的博客首页 (0 bytes) () 07/11/2014 postreply 10:50:29

• 公理的意思是我们不能证明是正确，也不能证明它是错的 -littlecat8- ♂ 给 littlecat8 发送悄悄话 littlecat8 的博客首页 (260 bytes) () 07/11/2014 postreply 10:58:51

请您先登陆，再发跟帖！