Theorem 2: Commutativity of addition: 
Proof: Base case: By lemma 1,  .
.
- Inductive hypothesis: Suppose that, for
 ,
,  .
. - By axiom 6,
 .
. - By theorem 1,
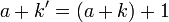 .
. - By the inductive hypothesis,
 .
. - By theorem 1,
 .
. - By lemma 1,
 .
. - By theorem 1,
 .
. - By axiom 6,
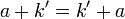 .
. - By induction,
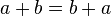 . QED.
. QED.