量子態
| 量子力學 | ||||||||
 |
||||||||
| 不確定性原理 |
||||||||
入門、數學表述
|
||||||||
在量子力學裏,量子態抽象地設定了一個量子系統的物理狀態。當我們描述一個量子系統時,我們希望能夠既簡易、又明確地描述這個量子系統的各種物理狀態,怎樣從一個物理狀態變換到另外一個物理狀態。量子態的概念可以幫助我們達到這目標。量子態是一個抽象的術語。我們用量子態來表明,一個量子系統的物理狀態。
每一個量子態都可以用存在於希爾伯特空間的態向量來表示。有時候,因為物理作用,一個量子態會變換到另外一個量子態。這過程可以用態向量的數學來表達。物理學家常用狄拉克標記來標記量子態或態向量。量子態或態向量的線性組合可以描述量子態的干涉現象。
目录[隐藏] |
[编辑] 概念
[编辑] 物理狀態
讓我們先從經典力學的一個例子,來探索一個物理系統的狀態與相關概念。試想一個物理系統,裡面有一個質量為 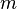 的粒子,自由地移動於一維空間。假設,在時間
的粒子,自由地移動於一維空間。假設,在時間 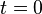 ,粒子的位置
,粒子的位置 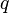 是
是  ,動量
,動量 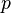 是
是  。這些初始條件設定了系統的狀態
。這些初始條件設定了系統的狀態  ,標記為
,標記為  。
。
過一段時間,在  ,我們試著測量這粒子的運動參數。在這個簡單的物理系統裏,我們能夠測量的物理量,基本上是它的位置
,我們試著測量這粒子的運動參數。在這個簡單的物理系統裏,我們能夠測量的物理量,基本上是它的位置  與動量
與動量  。其它物理量的都是這兩個物理量的函數。這裏,我們稱可以被測量的物理量為可觀察量。
。其它物理量的都是這兩個物理量的函數。這裏,我們稱可以被測量的物理量為可觀察量。
知道系統在 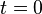 狀態
狀態  ,應用牛頓運動定律,我們可以計算出可觀察量在任何時間
,應用牛頓運動定律,我們可以計算出可觀察量在任何時間  的量值。這量值應該完全符合我們測量的結果。標記這些計算的量值為
的量值。這量值應該完全符合我們測量的結果。標記這些計算的量值為  與
與  。 在我們這個簡單的例子裏,粒子以等速移動。因此
。 在我們這個簡單的例子裏,粒子以等速移動。因此
 ,
, 。
。
現在,假設粒子的位置的初始條件是機率密度函數  ,動量的初始條件是機率分佈函數
,動量的初始條件是機率分佈函數  。這兩個機率分佈函數完全地描述這物理系統的狀態
。這兩個機率分佈函數完全地描述這物理系統的狀態  。可觀察量
。可觀察量  與
與  變成隨機變量。任何測量的結果都是隨機的,無法準確地預測。可是,假若,給予一個系綜的同樣的物理系統,對於每一個物理系統做同樣的測量,得到的結果會呈機率分佈。我們可以預測可觀察量在
變成隨機變量。任何測量的結果都是隨機的,無法準確地預測。可是,假若,給予一個系綜的同樣的物理系統,對於每一個物理系統做同樣的測量,得到的結果會呈機率分佈。我們可以預測可觀察量在  狀態的期望值。標記
狀態的期望值。標記  的期望值為
的期望值為  。
。
[编辑] 量子態
一個量子態的某些性質,可以經過測量而得知其物理量。這些可以得知的物理量,稱為可觀察量。所有可觀察量的機率分佈設定了量子系統的量子態。
[编辑] 本徵態
假若,對於許多同樣的量子態的某一個可觀察量做測量,結果都一樣。那麼,這量子態是這個可觀察量的本徵態,又稱確定態。量子態可以是幾個本徵態的疊加。一個可觀察量的本徵態可能不是另外一個可觀察量的本徵態。既然,實際上,我們只能得知一個量子系統的每一個可觀察量。
假若,一個量子態不是一個可觀察量的本徵態,對於這量子態的這個可觀察量的測量,答案是機率性的;也就是說,給予一個系綜許多相同的量子系統,每一個量子系統的量子態都一樣,都是某個可觀察量的很多不同的本徵態的疊加,對於這可觀察量做同樣的測量,獲得的答案可以表達為機率分佈。這是量子力學與經典力學之間,大不相同的一點。在經典力學裏,測量的結果本質上是決定性的,而不是機率性的。
對於任何可觀察量  ,我們通常可以製備一個本徵態
,我們通常可以製備一個本徵態  。對於這本徵態
。對於這本徵態  的可觀察量
的可觀察量  所做的一個測量,獲得的結果是明確的。給予一系綜這樣的系統,對於每一個本徵態
所做的一個測量,獲得的結果是明確的。給予一系綜這樣的系統,對於每一個本徵態  的可觀察量
的可觀察量  所做的測量,答案都是一樣的。本徵態
所做的測量,答案都是一樣的。本徵態  又稱為
又稱為  的本徵態。
的本徵態。
假設一個量子系統的量子態 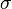 原本不是
原本不是  的本徵態。那麼,對於這量子態的可觀察量
的本徵態。那麼,對於這量子態的可觀察量  所做的一個測量,會將量子態塌縮為
所做的一個測量,會將量子態塌縮為  的一個本徵態
的一個本徵態  ,測量的結果是這本徵態的本徵值
,測量的結果是這本徵態的本徵值  。假若我們立刻再測量可觀察量
。假若我們立刻再測量可觀察量  ,由於量子態仍舊是同樣的本徵態
,由於量子態仍舊是同樣的本徵態  ,所得到的測量值也是同樣的本徵值
,所得到的測量值也是同樣的本徵值  。
。
思考兩個不相容可觀察量  與
與  。假設一個量子系統原本處於
。假設一個量子系統原本處於  的本徵態
的本徵態  。假若我們只測量
。假若我們只測量  ,我們不會發現到任何統計行為。可是假若我們先測量
,我們不會發現到任何統計行為。可是假若我們先測量  ,量子系統會塌縮成
,量子系統會塌縮成  的本徵態
的本徵態  。假若,我們立刻再測量
。假若,我們立刻再測量  ,我們會得到統計性的答案。
,我們會得到統計性的答案。
[编辑] 薛丁格繪景或海森堡繪景
在前面的講述,可觀察量  ,
,  可以相依於時間,而量子態
可以相依於時間,而量子態 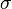 則不相依於時間。這方法稱為海森堡繪景。我們可以等價地使可觀察量不相依於時間,又使量子態相依於時間。這方法是薛丁格繪景。概念上,這兩種繪景是等價地。兩種繪景都常常用在量子力學。非相對論性量子力學通常表述於薛丁格繪景,而在相對論性狀況,像是量子場論,則海森堡繪景是比較喜好的方法。
則不相依於時間。這方法稱為海森堡繪景。我們可以等價地使可觀察量不相依於時間,又使量子態相依於時間。這方法是薛丁格繪景。概念上,這兩種繪景是等價地。兩種繪景都常常用在量子力學。非相對論性量子力學通常表述於薛丁格繪景,而在相對論性狀況,像是量子場論,則海森堡繪景是比較喜好的方法。
[编辑] 量子力學形式論
[编辑] 量子態是希爾伯特空間的射線
量子力學通常表述於線性代數。在一個量子系統裏,每一個量子態都對應於希爾伯特空間的一個向量,稱為態向量。假若,一個向量是另外一個向量的標量倍數,則這兩個向量都對應於同樣的量子態。(換句話說,每一個量子態都是希爾伯特空間的一個射線)。
或者,我們只准許歸一化的向量代表量子態。這樣,所有量子態的集合對應於希爾伯特空間的單位球。假若,兩個歸一化態向量,唯一的不同處是它們的相位因子。那麼,這兩個態向量仍舊對應於同樣的量子態。
[编辑] 狄拉克標記
在量子力學裏,數學運算時常用到線性算符,內積,對偶空間,與厄米共軛。為了讓運算更加簡易,避免更深入研讀線性代數的需要,保羅·狄拉克發明了一種標記法,狄拉克標記。這標記法能夠精確地表達量子態。簡略表述如下:
- 向量標記形式為
 ;其中
;其中 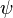 可以用任何符號,字母,數字,或單字。這與通常的數學標記顯然地不同。通常,向量以粗體字母,或者在上方加了一支矢號的字母來標記。
可以用任何符號,字母,數字,或單字。這與通常的數學標記顯然地不同。通常,向量以粗體字母,或者在上方加了一支矢號的字母來標記。 - 稱向量為右括向量。
- 每一個右括向量
 ,都獨特地伴隨一個左括向量
,都獨特地伴隨一個左括向量  ,這兩個向量都對應於同樣的量子態。
,這兩個向量都對應於同樣的量子態。 - 兩個向量的內積,可以寫為
 。
。
[编辑] 單粒子系統的基底量子態
與任何向量空間一樣,設定一個希爾伯特空間的正交歸一的基底量子態, 。那麼,任何右括向量
。那麼,任何右括向量  可以展開為這基底量子態的線性組合。
可以展開為這基底量子態的線性組合。
 ;
;
其中,係數  是複值係數。
是複值係數。
用物理術語來描述,  是量子態
是量子態  的疊加。由於這基底滿足正交歸一性,
的疊加。由於這基底滿足正交歸一性,
 ,
, 。
。
在量子力學的測量問題裏,這種展開式佔有很重要的角色。特別是,假若  是一個可觀察量
是一個可觀察量  的本徵值為
的本徵值為  的本徵態。那麼,對於量子態
的本徵態。那麼,對於量子態  的可觀察量
的可觀察量  的一個測量,得到的結果為
的一個測量,得到的結果為  的機率是
的機率是 。
。
一個常見的例子是位置基底。這個基底是由位置這可觀察量的本徵態構成的。假若這些本徵態是不兼併的,那麼,每一個右括向量  都對應於一個三維空間的複值函數:
都對應於一個三維空間的複值函數:
 。
。
這函數稱為對應於  的波函數。
的波函數。
[编辑] 態疊加原理
設定  and
and  為兩個不同的量子態。它們的線性疊加
為兩個不同的量子態。它們的線性疊加  是另外一個量子態(尚未歸一化)。思考
是另外一個量子態(尚未歸一化)。思考 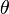 為實值的量子態
為實值的量子態  ,雖然與
,雖然與  對應於同樣的量子態,他們並無法互相替換。可是,
對應於同樣的量子態,他們並無法互相替換。可是,  和
和  肯定地對應於同樣的量子態。我們可以這樣說,整體的相位因子並無物理性質,但相對的相位因子的物理性質很重要。
肯定地對應於同樣的量子態。我們可以這樣說,整體的相位因子並無物理性質,但相對的相位因子的物理性質很重要。
例如,在雙縫實驗裏,光子的量子態是兩個不同的量子態的疊加。其中一個是通過狹縫 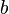 的量子態。另外一個是通過狹縫
的量子態。另外一個是通過狹縫  的量子態。光子抵達偵測屏障的位置
的量子態。光子抵達偵測屏障的位置  ,這位置離開兩條狹縫的距離之差值
,這位置離開兩條狹縫的距離之差值  ,與兩個量子態的相對的相位有關。而這相對的相位,在偵測屏障的某些位置,又造成了建設性干涉,或摧毀性干涉。
,與兩個量子態的相對的相位有關。而這相對的相位,在偵測屏障的某些位置,又造成了建設性干涉,或摧毀性干涉。
另外一個例子,拉比振動,可以顯示出相對相位在量子態疊加中的重要性。這是一個雙態系統。假若系統的兩個本徵態的本徵能級不一樣,那麼,因為態疊加的相對相位隨著時間而改變,疊加後的量子態會反來復去的震動於兩個本徵態的線性組合。
[编辑] 純態與混態
前面所講述的量子態都是純態,可以用一個右括向量來代表。一個混態是一個系綜的純態。混態是用一個密度矩陣,或密度算符,來描述。密度矩陣可以描述純態和混態。用方程式來定義,
 ;
;
其中, 是密度矩陣,
是密度矩陣, 是純態
是純態  在系綜裏所佔的比例。
在系綜裏所佔的比例。
我們可以用一個很簡單的公式,來判斷一個密度矩陣,到底是描述純態還是混態。首先,必須將量子態歸一化。假若,矩陣的跡值  ,則所描述的是純態;否則,假若
,則所描述的是純態;否則,假若  ,則所描述的是混態。另外一個等價的判斷式用馮諾伊曼熵來決定量子態的種類:純態的馮諾伊曼熵是 0 ;而混態的馮諾伊曼熵則大於 0 。
,則所描述的是混態。另外一個等價的判斷式用馮諾伊曼熵來決定量子態的種類:純態的馮諾伊曼熵是 0 ;而混態的馮諾伊曼熵則大於 0 。
在量子力學裏,測量的規則可以特別簡單的用密度矩陣來表達。舉例而言,對應於一個可觀察量  的一個測量的期望值是
的一個測量的期望值是
 ;
;
其中, 是
是 的本徵態,
的本徵態,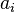 是本徵值。
是本徵值。
特別注意,在這裏,一共發生了兩種不同的平均運算。一種是純態的基底右括向量  的量子平均。另外一種是個統計平均,每一個量子態
的量子平均。另外一種是個統計平均,每一個量子態  的機率是
的機率是  。
。
我們也可以用這些不同的平均運算,來判斷純態或混態:純態是量子態相干的疊加;而混態是量子態不相干的疊加

 。在擋牆的後面,設立了一個照相底片或某種偵測屏障
。在擋牆的後面,設立了一個照相底片或某種偵測屏障  ,用來紀錄到達
,用來紀錄到達