如图,将三角形ABD翻折并旋转至AEM(M即D),将三角形ADC翻折并旋转至AEN(N即D),由(2)中条件知,M,A,N三点共线,因为EM=BD=DC=FN,角EMA=角ADB,角ANF=角ADC,所以角EMA+角ANF=180度,即EFNM是平行四边形,这也顺便证明了(2)的结论,所以A是MN的中点,又G是EF的中点,即EGAM也是平行四边形,由此得角EAB=角MEA=60度,因为角EAM+角FAN+角EAB+角BAC+角CAF=180度,即 2*角BAC+60度+角CAF=180度,可得 角BAC=60度-角CAF/2,即角GAF=角BAC+角CAF=60度-角CAF/2+角CAF=60度+角CAF/2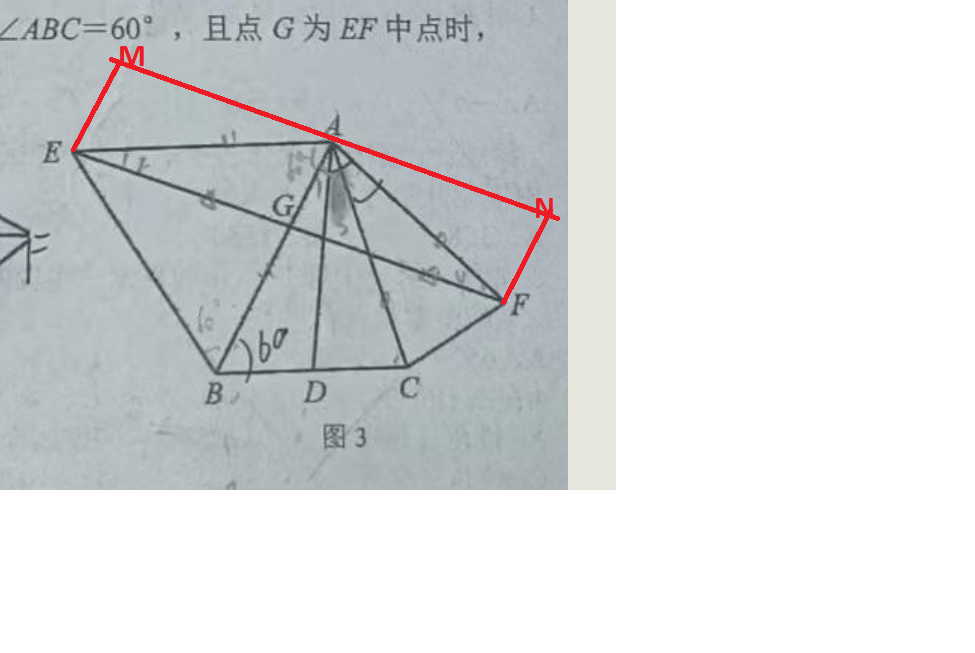
证明过程
所有跟帖:
•
国内的数学作业都这么难了,匪夷所思。谢谢!!!看到你的答案,想的是作CF的中垂线AH来证角GAH=60.
-wxcfan123-
♂
![]() (0 bytes)
()
04/21/2024 postreply
17:58:35
(0 bytes)
()
04/21/2024 postreply
17:58:35