本文只是我身为一个【读英国Alevel高中课程,但是准备申请美国大学】的高中生,对于英美教育的一点愚见。转载请注明原作者。
作为一个美式教育的亲历者,我不想为美国的数学基础教育做任何辩护。
美国的中小学理科教育质量非常差,这是不争的事实。
但是!既然美国理科基础教育质量那么差,为什么它能包揽364个诺贝尔奖,33个菲尔兹奖,37个图灵奖?它又是怎么做出无数最先进的科研成果,建立起高科技事业云集,还有坐拥全美三分之一风险投资总额的硅谷?
这其中很大一部分都得归功于美国一个秘密武器,那就是H-1B。

且不论硅谷里面外籍员工的比例,光全美博士生就有超过一半都是外籍:美国这个国家就像是一个巨大的磁铁一样把全世界的人才都吸过去了。
物理学家加来道雄曾经在一次辩论中提到
"The Wall Street Journal editorialised against the congressman who wanted to ban the H-1B saying it will take jobs from the American people. The Wall Street Journal said: look, there are no Americans who can take these jobs. They are at the highest level of high technology. They don't take away jobs from Americans - they create entire industries."
「华尔街日报曾反驳过一个认为H-1B会夺走美国人的工作而支持废除H-1B的议员。华尔街日报说:根本没有美国人有能力做这些工作,这些都是高科技产业里面最尖端的工作。不是他们抢走了美国人的工作,而是整个产业都是他们创造出来的。」
大批亚洲和欧洲的人才拿着H-1B签证到美国做着最最顶尖的科学研究,这就是美国拥有糟糕的科学基础教育却有雄厚的科研实力的根本原因:它靠绿卡和移民优惠让全世界最牛逼的科学家们给它打工。
但是美国科研实力强,还有另外一个原因。这个原因也是我最有切身体会的一个,那就是美国(英国也一样)的教育资源的分配非常不均。往往是少数精英阶级占用了最优的教育资源,大多数美国人得不到接受优质教育的机会。
即使在中学阶段,美国学生和学生之间早有了鲜明的阶级分层了。公立学校的学生放学以后高高兴兴的回家的时候,私立学校的学生仍然要参加各种补习班。在英国,任意找一个公立学校的学生和伊顿公学的学生比一比,高下立判。
伊顿公学的招生官曾经在我们高中宣讲中提到了伊顿对于学生的选拔和管理:伊顿的初中招生是提前4年在学生9岁的时候就要报名,经过多层考试选拔出来的。学校全宿舍制,全军事化管理,每年从1000个申请者中录取250个,这250个人在6年后有28%都考入牛津剑桥,另外还有42%考入牛剑以外的世界名校。虽然说并没有到衡水一中的那种程度,但是大多数英国私立学校的学生都是不轻松的,每个学生肩上都有巨大的压力。
美国也是一样,有着Phillips Academy Andover,Lawrenceville School,Phillips Exeter Academy这样33%学生进入常春藤,斯坦福,MIT的精英阶级高中。这几个学校的旧SAT平均分,保守估计不会低于2100/2400分,尚且不说这里面优秀的学生个个都以SAT满分为目标。(SAT和ACT相当于美国的高考,考察英语阅读,语法,作文以及数学。旧SAT满分2400,新SAT满分1600,ACT满分36。)
私立学校的学生早就不拘泥于课本了。英美的优秀私立高中里,高中生学微积分和线性代数是再平常不过的事情了。公立学校的学生还在对着Algebra II发愁的时候,私立学校的学生早早就拿下了AP Calculus BC的5分(我见过最夸张的一个修了12门AP最后高三一共拿了9个5分)。这就导致了一个现象,那就是你会发现美国好像全国的智商都被精英阶级吸走了。
我们看一组CollegeBoard的统计数据,这是学生平均SAT成绩和其家庭收入的关系

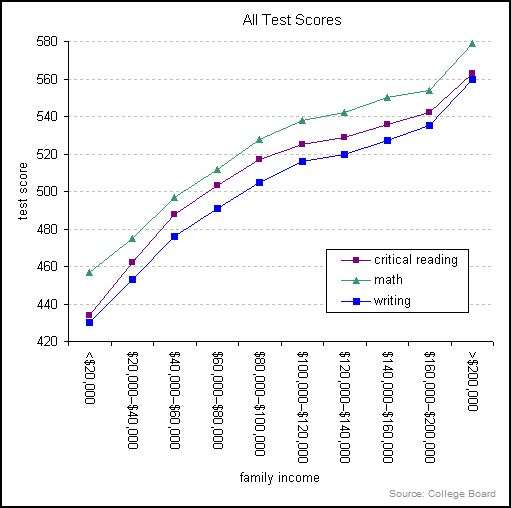
学生的SAT成绩和学生家庭的收入有非常强的正相关性。
英国也有相同的问题。
我现在读的就是英国Alevel高中课程系统,Alevel的数学分成数学和进阶数学两个科目。
Alevel数学包括了中国高中数学大多数的知识点(纯数学卷+力学卷+统计卷)。用向量解决三维几何问题啊,基本的复数知识啊,数列啊,函数啊,还包括了一点基础的微积分,等等。另外还有两卷分别考统计(基本概率论,排列组合,正态分布,二项分布等等)还有力学(连接体,抛体,圆周运动等等)。
我从近几年的数学随便挑了两道题,可以和后面对比一下难度
【例一】
1.分别计算 和
的模和幅角
2.在复平面上画出 和
,并把同时满足
和
的复数的区域涂上阴影
【例二】
空间中有 四点,已知
求:
1.包含 三点的平面方程,写成
形式
2. 是
到该平面的垂线的垂足,求出
,并求出
的长度
【例三】
已知 ,
满足
1.证明 并求出
2.已知 ,不使用计算器,求
的值
进阶数学的难度就比数学大很多了。它包括了一些中国大学里面才会讲的微积分,线代,统计,和复变知识。二阶齐次线性微分方程,矩阵的特征分解,行列式,复变的欧拉公式以及利用其解决三角函数问题,还会结合微积分考察数学归纳法的运用等等;统计卷则会考假设检验,T分布,负指数分布,几何分布,置信区间,卡方检验,线性回归,还会让你用微积分算PDF和CDF;力学则会有简谐运动,转动惯量,比较复杂的碰撞问题和刚体平衡问题。此外,虽然不考,但是课本上也有群论之类更深的数学知识。
进阶数学的题目是这样的
【例一】
已知 ,且
证明
是横轴与
从
到
包围的区域,计算
的质心的纵坐标
【例二】
已知 不是
的整数倍,不使用数学归纳法,证明
进而证明
又已知 ,证明
【例三】
考虑两个线性变换 以及
分别对应矩阵
和
是
的值域空间,
是
的零空间,
是所有属于
但不属于
的向量的集合,
是先应用
再应用
的线性变换。
求:
1. 的一组基
2. 的一组基,并证明
是
的子空间
3. 是不是一个向量空间?证明你的回答
4. 的零空间的维度
但是最优秀的那1%的英国学生都会选择去考MAT和STEP,这两个考试是专门为想要考牛津,剑桥,帝国理工,华威,UCL这种学校的学生设计的。题目难度跟进阶数学天差地别,而且方法更复杂,套路少,灵活度大。
【例一】
对于正整数 和
(满足
),
定义为大于
并小于等于
的所有质数的积,如果没有质数满足大于
小于等于
,那么
1.证明 对于任意正整数
成立(
代表
个物体选
个有多少种选法)
2.证明,对于任意正整数 ,有
整除
,并证明
3.证明,如果当 时有
,就有
4.证明,当 时,
【例二】
证明
【例三】
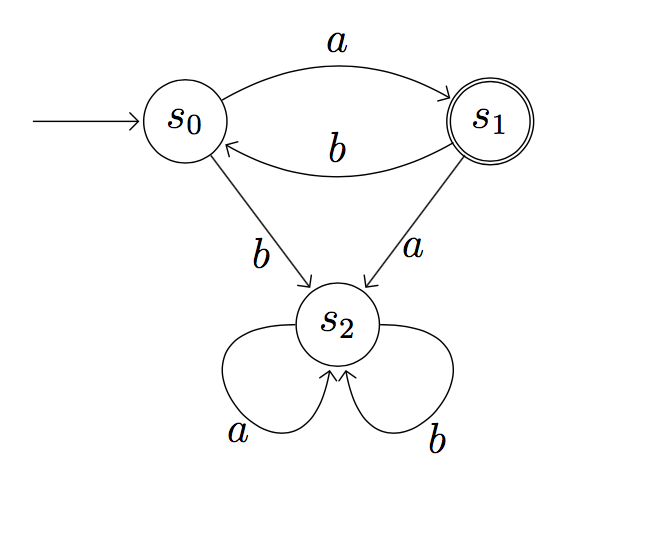
一个finite automation是一个拥有有限个状态的模型。上图是一个finite automation的例子,它有三种状态, ,
和
。从
开始,输入
或者
,其状态会根据箭头指向的状态改变。一些状态可以被设置为accepting state,用两个圈表示,这里
是一个accepting state,当状态改变到一个accepting state就会接受之前所有的输入组成的序列,这种序列被称为一个短语。例如,上图中的finite automation就能够接受"
"这个短语。
1.描述图中finite automation所接受的短语
2.如果将 ,
设定为accepting state,
为non-accepting state,描述该finite automation所接受的短语
3.画出一个finite automation,使其能够接受且只接受所有满足有偶数个 (包括0个)或者有奇数个
的短语
4.如果用 代表连续输入
次
,定义
为短语
(
),证明不存在一个finite automation能够接受且只接受
很明显能够看出,从Alevel数学,Alevel进阶数学,到MAT以及STEP,难度是成几何增长的。从英国学生对这三个考试的选择,很容易看学生之间的差距。一些学生高二还在学Alevel数学P3的时候,很多私立学校已经把这两年的课程压缩到一年甚至一个学期学完,学进阶数学去了。而美国的情况则更极端一点。美国高考SAT/ACT数学的题目,我也不翻译了,随便挑几道你们感受一下。
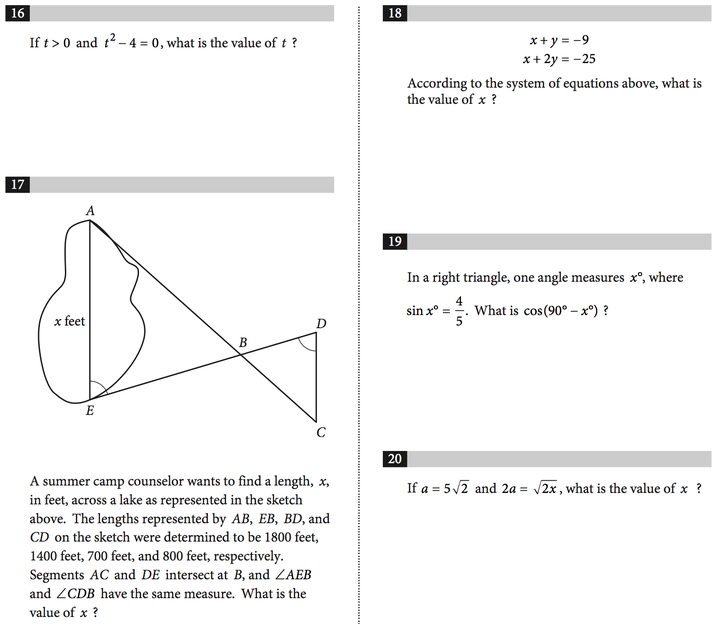
简单吧?SAT的数学部分大多数中国学生最后都能拿到750分以上的成绩(满分800),而最新的一次美国本土的平均分是541分。本土数学厉害的学生则都走了竞赛路线,考AMC,AIME,USAMO去了。
所以可以看出,美国学生两极分化严重,数学差得很差,但有少数数学厉害的,那可是相当厉害:最后“做出超级牛的东西”的往往是后者。
总结:
「为什么美国中小学生学的数学比我们简单,美国人却还能做出超级牛的东西?」
1.不同阶级家庭出来的学生的数学天差地别,精英阶级不少学生数学非常厉害,他们的数学一点都不简单。
2.美国靠福利吸引了很多外籍优秀人才,他们为美国很多高科技产业贡献巨大,同时给美国提供了很多优秀的教育资源。
先说这么多。
=====================
评论区
关于竞赛的问题。
我本人竞赛经验很少,对于学科竞赛了解非常浅薄,很有可能有说错的地方,所以上面我基本没有把竞赛放在讨论范围内。
美国有很多是大学自己办的数学竞赛,斯坦福的Stanford Math Tournament,普林斯顿的PuMac,哈佛和麻省理工的HMMT等等。很多学生并不是全职去竞赛的,而是偶尔参加一下这种大学自主举办的竞赛,主要目的只是拿个名次让自己的大学Application好看一点(当然他们仍然需要考高考(SAT/ACT),做社会实践啊啥的)。这类竞赛就有可能会涉及到高等数学。
而像奥林匹克学科竞赛,USAMO,AMC/AIME这种,我感觉更多是用初等的方法证明高等数学得到的结论的特殊情况,会学到用到很多巧方法。参加的人也一般会休学备考,全身心投入竞赛。
前者以及我提到的Alevel进阶数学,STEP,MAT,和奥林匹克竞赛的题型有着本质上的不同。如果让这两类学生互相做对方的题目,很大可能两方都做不出来。
但是其实奥赛里面教的很多方法都是有很深刻的高等数学思想的。比如说一些高考压轴题和联赛试题的出题人可能会选择从某个数学分支学科挑出一个结论的特殊情况,这个特殊情况能够用初等数学方法解决,然后用它来出题。我之前在斯坦福上夏校的时候,当时是一个斯坦福的数学Ph.D Candidate给我们lecture,我问了他一个类似的问题,他当时在黑板上画了这么一个示意图:
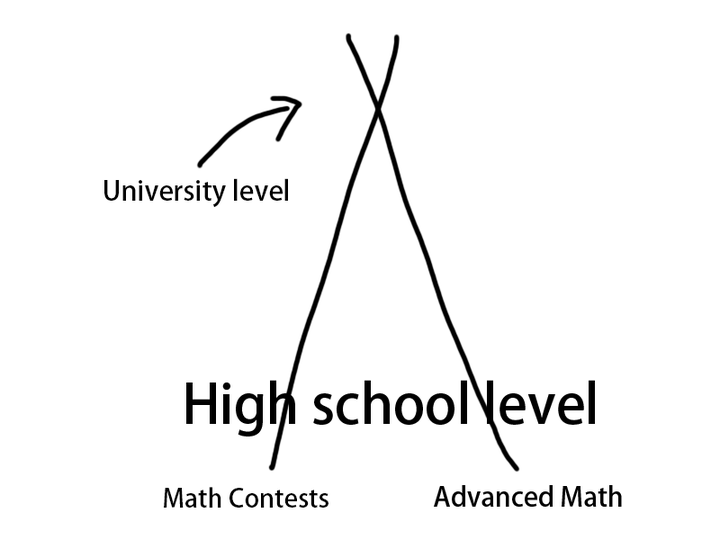
意思大概是,选择奥赛或者高等数学两条路的学生虽然在高中阶段有较大区别,但是到大学更往上的阶段就会有交点了。我觉得他说的很对。其实不是两者没有交点,只不过交点非常不明显罢了,需要我们进入大学对数学有更深理解的以后才能明白。
作者:Daniel Xiang
链接:https://www.zhihu.com/question/20953633/answer/212652061
来源:知乎
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。