微分几何/切向量與正則曲線
有了參數式後,我們就不可免除的要來微分一下,我們稱  的一階導數
的一階導數  為曲線
為曲線 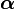 於 t 的切向量(或速度向量,以物理學的角度來看)。若切向量
於 t 的切向量(或速度向量,以物理學的角度來看)。若切向量  ,則我們定義過
,則我們定義過  方向向
方向向  的直線為
的直線為 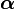 在
在 的切線,並且我們可定義單位切向量
的切線,並且我們可定義單位切向量  為與切向量同向而長度為1之向量。
為與切向量同向而長度為1之向量。
有時我們會發現,光有可微性仍然無法保證曲線能長得很平滑,如以下這個例子:
例:  。
。
這個例子中,我們可以看到曲線上會有一個轉折。探究原因,我們發現在  這點,切向量
這點,切向量  ,我們稱這種切向量(一階導數)等於零的點為奇點。若我們把單位切向量函數
,我們稱這種切向量(一階導數)等於零的點為奇點。若我們把單位切向量函數  的參數 t 對 0 作逼近,我們會發現其左極限和右極限是不相等的,即是說奇點的存在容許了這種單位切向量的轉折,也因此奇點的切線是未定義的。為了確保切線能存在,我們便定義正則曲線:
的參數 t 對 0 作逼近,我們會發現其左極限和右極限是不相等的,即是說奇點的存在容許了這種單位切向量的轉折,也因此奇點的切線是未定義的。為了確保切線能存在,我們便定義正則曲線:
定義: 一個可微參數曲線  為正則曲線,當
為正則曲線,當  對於所有
對於所有  。
。