弧长参数01 弧长参数作为折线的坐标卡，曲線線段的弧長跟所取得曲線參數無關

来源: marketreflections 于 2011-07-03 07:44:27 [档案] [博客] [旧帖] [给我悄悄话] 阅读数 : (4694 bytes)

回答: 拉普拉斯：世界线的长度是不变量，世界线是会随着参考系的不同而变化的，但其长度不变。世界线的“长度”是在闵氏空间的长度，和你在时空由 marketreflections 于 2011-07-03 07:28:25

微分幾何/弧長與弧長參數

维基教科书，自由的教学读本

跳转到：导航, 搜索

我們知道直線段的長度怎麼算： $L(\overline{AB})=\vert (x_A,y_A,z_A)-(x_B,y_B,z_B)\vert=\sqrt{(x_A-x_B)^2+(y_A-y_B)^2+(z_A-z_B)^2}$ 。因此我們可以用直線逼近的方式來定義曲線的弧長。

定義： 曲線 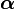$\boldsymbol{\alpha}$ 在區間 $[a,b]\subset I$ 的弧長為 $L(\boldsymbol{\alpha},[a,b])=\sup_{\lbrace t_k \rbrace_n} \sum_{k=1}^{n}\vert\boldsymbol{\alpha}(t_k)-\boldsymbol{\alpha}(t_{k-1})\vert$ ，其中 ${t k} n$ 為 $[a, b]$ 的分割。若曲線可微，則我們可以得 $L(\boldsymbol{\alpha},[a,b])=\int_{a}^{b} \vert\boldsymbol{\alpha}^\prime(t)\vert\, dt$ 。

若我們試著改變曲線參數，新參數 $u = u (t)$ 可微且嚴格遞增，而 $\boldsymbol{\alpha}_u (u(t))=\boldsymbol{\alpha}(t)$ ，我們對新的參數算弧長 $L(\boldsymbol{\alpha}_u,[u(a),u(b)])=\int_{u(a)}^{u(b)} \vert\boldsymbol{\alpha}_u^\prime\vert\, du=\int_{u(a)}^{u(b)} \vert\boldsymbol{\alpha}^\prime\vert \vert \frac{dt}{du} \vert \, du=\int_{u(a)}^{u(b)} \vert\boldsymbol{\alpha}^\prime\vert \frac{dt}{du} \, du=\int_{a}^{b} \vert\boldsymbol{\alpha}^\prime\vert\, dt=L(\boldsymbol{\alpha},[a,b])$ 。由此我們發現，曲線線段的弧長跟所取得曲線參數無關。

由於上述結果，我們可以對任意正則曲線取弧長參數， $s(t)=\int_{t_0}^{t} \vert\boldsymbol{\alpha}^\prime(t)\vert\, dt$ ，為。若我們將 $s$ 對 $t$ 微分 $\frac{ds}{dt}=\vert\boldsymbol{\alpha}^\prime(t)\vert$ ，假如 $t$ 也為弧長參數，則我們發現 $\vert\boldsymbol{\alpha}^\prime(t)\vert=\frac{ds}{dt}=1$ ；反過來說若 $\vert\boldsymbol{\alpha}^\prime(t)\vert=1$ ，則 $t = s + t 0$ 是弧長參數，即是說弧長參數與切向量長度等於 1 是充分必要條件。由於此方便的特性，我們往後會常使用弧長參數來探討曲線性質。

您的位置：文学城 » 论坛 » 音乐快递 » 弧长参数01 弧长参数作为折线的坐标卡，曲線線段的弧長跟所取得曲線參數無關

所有跟帖：

• 參數曲線 jw1.nwnu.edu.cn:8080/wfjh/adobe/11.pdf 曲線應該是在空間中的一種一維連續物件。而 -marketreflections- ♂ (1426 bytes) () 07/03/2011 postreply 07:53:37

请您先登陆，再发跟帖！