http://www.ccthere.com/article/2034749
公理 分别是：
公设1：任意一点到另外任意一点可以画直线。
公设2：一条有限线段可以继续延长。
公设3：以任意点为心及任意的距离可以画圆。
公设4：凡直角都彼此相等。
公设5：同平面内一条直线和另外两条直线相交，若在某一侧的两个内角和小于二直角的和，则这二直线经无限延长后在这一侧相交。
在这五个公设（理）里，欧几里德并没有幼稚地假定定义的存在和彼此相容。亚里士多德就指出，头三个公设说的是可以构造线和圆，所以他是对两件东西存在性的声明。事实上欧几里德用这种构造法证明很多命题。第五个公设非常啰嗦，没有前四个简洁好懂。声明的也不是存在的东西，而是欧几里德自己想的东西。这就足以说明他的天才。从欧几里德提出这个公理到1800年这大约2100年的时间里虽然人们没有怀疑整个体系的正确性，但是对这个第五公设却一直耿耿于怀。很多数学家想把这个公设从这个体系中去掉，但是几经努力而无果，无法从其他公设中推导出第五公设。
同时数学家们也注意到了这个公设既是对平行概念的论述（故称之为平行公理）也是对三角形内角和的论述（即内角和公理）。高斯对这一点是非常明白的，他认为欧几里德几何是物质空间的几何，1799年他说给他的朋友的一封信中表现了他相信平行公理不能从其他的公设中推导出来，他开始认真从事开发一个新的能够应用的几何。1813年，发展了他的几何，最初称为反欧氏几何，后称星空几何，最后称非欧几何。在他的几何中三角形内角可以大于180度。得到这样的几何的不是高斯一人，历史上有三个人。一个是他的搭档，另一个是高斯的朋友的儿子独立发现的。其中得到的一个有趣的结果是，非欧氏几何中过直线外一点的平行线可以无穷。
不久之后，俄国的罗巴切夫斯基也发现了一种新的非欧几何，即罗氏几何。他的三角形内角和是小于180度的。
而19世纪初非欧式几何的发现，正是后来爱因斯坦发现广义相对论的基础。
欧拉示性数
我们把球面几何和双曲几何放在一起看，有不少相似的“奇怪”性质。
球面几何里，（三条大圆弧构成的）三角形的内角和总大于180度。我们有
其中S是三角形面积，R是圆球半径，
是三角形内角。也就是说，内角和与180度的差与面积成正比，与半径平方成反比。
而在双曲几何里，三角形的内角和总小于180度。我们有
其中S是三角形面积，c是某个正的常数，
是三角形内角。内角和与180度的差还是与面积成正比。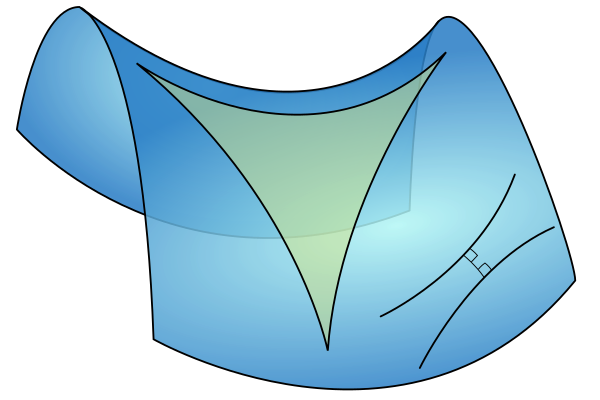
从这些公式可以看出，三角形的面积越小，它越像欧氏几何。今天的我们知道，之所谓我们感觉自己生活在欧氏空间里，是因为我们生活的尺度和宇宙比起来太小太小了。（各位有没有想起狭义相对论？）
再比如说我们已经遗忘很久的勾股定理。前面提到过，勾股定理与第五公设是等价的。也就是说，勾股定理正是欧式几何的“基石”之一。非欧几何里不再成立勾股定理。但直角三角形的三边a,b,c（斜边）还是有些特殊的关系。
球面几何中：Cos(a/R)Cos(b/R) = Cos(c/R)
双曲几何中：Cosh(a)Cosh(b) = Cosh(c)
不过，这还不是勾股定理最后一次出现，后面的篇章中，我们会看到勾股定理更深刻的意义。
类似的古怪公式不少，我就不一一列举了。
科学史上每次出现新生事物总有个被误解然后慢慢被承认的过程。牛顿的无穷小量也好，虚数也好，都在很长的时间里被人们视为“幽灵”。罗巴切夫斯基发现了新的几何后，自己也觉得这个东西实在太古怪。他把这种几何称为“想象的几何”。要人们接受这种想象的几何实在不容易。罗巴切夫斯基试图将双曲几何和人们熟悉的球面几何联系起来，说服人们双曲几何只是球面几何的一个兄弟。他的想法是正确的，但他并未完全成功。
我们的主人公们虽然发现了好东西，可它实在古怪，令人难以相信。伟大的理论还需要优秀的推销员。爱因斯坦碰上了爱丁顿爵士（Sir Arthur Stanley Eddington），让广义相对论少受了几年委屈。若干年后，非欧几何终于迎来了一位好推销员 ------ 意大利数学家贝尔特拉米（Eugene Beltrami）。
