生命和理由 (3): 生命方程
任给一个结构 f(x,y), 如果它是理性结构(rational structure),那么它必定存在等比例曲线。 今天,我终于找到等比例曲线的存在所必须满足的方程。令人惊讶的是,此方程简化成一个代数方程。是一个一元三次代数方程 (Cubic Equation):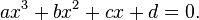
维基百科(Wikipedia)有专门的单元讨论一元三次代数方程:
cubic function
今天重温维基一元三次代数方程,使我回想起三十多年前的文革时代。1977年底的首届高考前夕,为了以防万一,我竟然初略地看过一元三次代数方程。
但是,上述一元三次代数方程只是理性结构的必要条件。判断一个矢量场是否有积分且积分曲线是否对应于一个正交曲线簇,我还真的没有多少知识。
我真希望建立一个公司,让大家参与探索星系及生命。
我已经决定把上述一元三次代数方程称为生命方程。
我的下一篇学术论文的标题就是生命方程(Life Equation),不管杂志是否接收我的论文。
我已经准备着再投稿一百次!
谈到生命和代数方程,大家千万不要忘记这个年轻生命:伽罗华
就是他,证明了五次以上代数方程没有公式解。他(21岁)在同情敌决斗前,“非常清楚对手的枪法很好,自己难以摆脱死亡的命运,所以连夜给朋友写信,仓促地把自己生平的数学研究心得扼要写出,并附以论文手稿。”
1985年上半年,我选修了伽罗华理论这门课,累得半死,才弄清楚如何证明五次以上代数方程没有公式解!
大家也不要忘记另一个年轻生命:拉马努金(印度千年一遇的数学家):

|
|
|
|
|
|
|
|
|
|