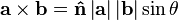vector01 由于向量的叉积由坐标系确定，所以其结果被称为伪向量;特征向量不是一个向量而是一个向量族

来源: marketreflections 于 2011-12-13 16:10:51 [博客] [旧帖] [给我悄悄话] 本文已被阅读：次

笔记本分享http://blog.sciencenet.cn/u/gosci 上善若水

博文

[转载]n维向量

已有 1090 次阅读2010-4-18 17:33|个人分类:线性代数|系统分类:科研笔记

1.n维向量的几何意义是什么

很简单。只是因为我们处于三维空间，大于三维的度量不容易感知。
先从三维谈起，如向量{x1,x2,x3}在三维空间上必然可以分解为
{x1,x2,x3}=x1{1,0,0}+x2{0,1,0}+x3{0,0,1}
这三个分量{1,0,0}{0,1,0}{0,0,1}是线性无关的。而且是正交的。这样空间直角坐标系就有了基。这三个分量可以将任何三维向量线性表出。所以三维向量组成的几何空间其实可以用这三个基表达出任何三维向量。当然，向量和点对应，三维向量其实也是对应三维直角坐标系的一个点。
这样对于n维向量{x1,x2,...,xn}=x1{1,0,..,0}+...+xn{0,0,...,1}
其实在n维空间上就是由n个基构成的一个线性组合。换句话说，它也是其在n维直角坐标系中的一个点。当然，这里的直角的含义是，n个基两两正交。
按照你的要求我再说明白一点，一个n维向量其实就是一个n维欧式空间的一个点。只不过是有n个向量的。

http://zhidao.baidu.com/question/69597510.html?fr=qrl&cid=983&index=2&fr2=query

2.向量内积的几何意义？

一个向量a和一个单位向量e的内积的几何意义是a在e方向的投影向量。

http://zhidao.baidu.com/question/78429506.html?fr=qrl&cid=983&index=3&fr2=query

3. 特征值，特征向量是什么？

特征向量确实有很明确的几何意义，矩阵(既然讨论特征向量的问题，当然是方阵，这里不讨论广义特征向量的概念，就是一般的特征向量)乘以一个向量的结果仍是同维数的一个向量，因此，矩阵乘法对应了一个变换，把一个向量变成同维数的另一个向量，那么变换的效果是什么呢？这当然与方阵的构造有密切关系，比如可以取适当的二维方阵，使得这个变换的效果就是将平面上的二维向量逆时针旋转30度，这时我们可以问一个问题，有没有向量在这个变换下不改变方向呢？可以想一下，除了零向量，没有其他向量可以在平面上旋转30度而不改变方向的，所以这个变换对应的矩阵(或者说这个变换自身)没有特征向量(注意：特征向量不能是零向量)，所以一个变换的特征向量是这样一种向量，它经过这种特定的变换后保持方向不变，只是进行长度上的伸缩而已(再想想特征向量的原始定义Ax= cx,你就恍然大悟了,看到了吗？cx是方阵A对向量x进行变换后的结果，但显然cx和x的方向相同)，而且x是特征向量的话，ax也是特征向量(a是标量且不为零)，所以所谓的特征向量不是一个向量而是一个向量族，另外，特征值只不过反映了特征向量在变换时的伸缩倍数而已，对一个变换而言，特征向量指明的方向才是很重要的，特征值不是那么重要，虽然我们求这两个量时先求出特征值，但特征向量才是更本质的东西！

比如平面上的一个变换，把一个向量关于横轴做镜像对称变换，即保持一个向量的横坐标不变，但纵坐标取相反数，把这个变换表示为矩阵就是[1 0;0 -1]，其中分号表示换行，显然[1 0;0 -1]*[a b]'=[a -b]',其中上标'表示取转置，这正是我们想要的效果，那么现在可以猜一下了，这个矩阵的特征向量是什么?想想什么向量在这个变换下保持方向不变，显然，横轴上的向量在这个变换下保持方向不变(记住这个变换是镜像对称变换，那镜子表面上(横轴上)的向量当然不会变化)，所以可以直接猜测其特征向量是 [a 0]'(a不为0)，还有其他的吗？有，那就是纵轴上的向量，这时经过变换后，其方向反向，但仍在同一条轴上，所以也被认为是方向没有变化，所以[0 b]'(b不为0)也是其特征向量，去求求矩阵[1 0;0 -1]的特征向量就知道对不对了!

http://wenda.tianya.cn/wenda/thread?tid=4ed7c7f902bc1879

4.特征值特征向量的几何意义-2？

http://202.117.96.226:8090/xxds/swf/tezheng1.htm

5.向量积

向量积，也被称为叉积（即交叉乘积）、外积，是一种在向量空间中向量的二元运算。与点积不同，它的运算结果是一个伪向量而不是一个标量。并且两个向量的叉积与这两个向量都垂直。

定义

两个向量 a 和 b 的叉积写作 a × b （有时也被写成 a ∧ b，避免和字母 x 混淆）。叉积可以被定义为：

$\mathbf{a}\times\mathbf{b} = \mathbf\hat{n} \left| \mathbf{a} \right| \left| \mathbf{b} \right| \sin \theta$

在这里 θ 表示 a 和 b 之间的角度（0° ≤ θ ≤ 180°），它位于这两个矢量所定义的平面上。而 n 是一个与 a 和 b 均垂直的单位矢量。

这个定义有一个问题，就是同时有两个单位向量都垂直于 a 和 b：若 n 满足垂直的条件，那么 -n 也满足。

“正确”的向量由向量空间的方向确定，即按照给定直角坐标系 (i, j, k) 的左右手定则。若 (i, j, k) 满足右手定则，则 (a, b, a × b) 也满足右手定则；或者两者同时满足左手定则。

一个简单的确定满足“右手定则”的结果向量的方向的方法是这样的：若坐标系是满足右手定则的， $\mathbf{c} = \mathbf{a}\times\mathbf{b}$ 当右手的四指从a以不超过180度的转角转向b时，竖起的大拇指指向是c的方向。由于向量的叉积由坐标系确定，所以其结果被称为伪向量。