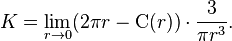对于平面曲线 C，在一点P的曲率大小等于密切圆半径的倒数，它是一个指向该圆圆心的向量。其大小可用屈光度（dioptre）衡量，1

对于平面曲线 C，在一点P的曲率大小等于密切圆（英语：Osculating circle）半径的倒数，它是一个指向该圆圆心的向量。其大小可用屈光度（dioptre）衡量，1屈光度等于1（弧度）每米。此密切圆的半径即为曲率半径。

密切圆的半径越小，曲率越大；所以曲线接近平直的时候，曲率接近0，而当曲线急速转弯时，曲率很大。

高斯曲率在一点P的内在定义的一种：想象一直用一条长为r的短线绑在P。她在线拉直的时候绕P点跑并测量绕P点的一圈的周长C(r)。如果曲面是平的，她会发现 C(r) = 2πr。在弯曲的曲面上，C(r)的公式不同，P点的高斯曲率 K可以这样计算：

高斯曲率在整个曲面上的积分和曲面的欧拉示性数有密切关联；参见高斯-博内定理。

平均曲率等于主曲率的和，k₁+k₂，除以 2。其单位为1／长度。平均曲率和曲面面积的第一变分密切相关，特别的，像肥皂膜这样的最小曲面平均曲率为0，而肥皂泡平均曲率为常数。不像高斯曲率，平均曲率依赖于嵌入，例如，一个圆柱和一个平面是局部等距的，但是平面的平均曲率为0，而圆柱的非零。