big spikes followed by big spikes, 加速度, GR, causing panic, gr 没有测度
廣義速度
维基百科,自由的百科全书
汉漢▼▲
为了阅读方便,本文使用全文手工轉換。转换内容:
- 原始语言:Gravitation;繁體:萬有引力;简体:万有引力; 当前用字模式下显示为→万有引力
- 原始语言:traction;繁體:牽引力;简体:牵引力; 当前用字模式下显示为→牵引力
- 原始语言:attraction;繁體:吸引力;简体:吸引力; 当前用字模式下显示为→吸引力
- 原始语言:Integral form;繁體:積分形式;简体:积分形式; 当前用字模式下显示为→积分形式
- 原始语言:Differential form;繁體:微分形式;简体:微分形式; 当前用字模式下显示为→微分形式
- 原始语言:Gravitational acceleration;繁體:重力加速度;简体:重力加速度; 当前用字模式下显示为→重力加速度
- 原始语言:equations;繁體:方程組;简体:方程组; 当前用字模式下显示为→方程组
- 原始语言:Auger;大陆:俄歇;台灣:奧杰; 当前用字模式下显示为→俄歇
- 原始语言:Avogadro constant;台灣:亞佛加厥常數;大陆:阿伏伽德罗常量;香港:阿佛加德羅常數; 当前用字模式下显示为→阿伏伽德罗常量
- 原始语言:Bohr magneton;大陆:玻尔磁子;台灣:波耳磁元; 当前用字模式下显示为→玻尔磁子
- 原始语言:Born-Oppenheimer approximation;大陆:玻恩-奥本海默近似;台灣:波恩-歐本海默近似法; 当前用字模式下显示为→玻恩-奥本海默近似
- 原始语言:Big Bang;大霹靂⇒简体:大爆炸;大霹靂⇒繁體:大爆炸;大霹靂⇒大陆:大爆炸;大霹靂⇒香港:大爆炸;大霹靂⇒新加坡:大爆炸;大霹靂⇒台灣:大爆炸; 当前用字模式下显示为→大爆炸
- 原始语言:Big Bang;台灣:大爆炸;大陆:大爆炸;香港:大爆炸;新加坡:大爆炸; 当前用字模式下显示为→大爆炸
- 原始语言:Biot-Savart law;台灣:必歐-沙伐定律;大陆:毕奥-萨伐尔定律; 当前用字模式下显示为→毕奥-萨伐尔定律
- 原始语言:Boltzmann constant;大陆:玻尔兹曼常量;台灣:波茲曼常數; 当前用字模式下显示为→玻尔兹曼常量
- 原始语言:Brackett series;大陆:布拉开线系;台灣:布拉克系; 当前用字模式下显示为→布拉开线系
- 原始语言:Brans-Dicke (theory);大陆:布兰斯-迪克;台灣:卜然斯-狄基; 当前用字模式下显示为→布兰斯-迪克
- 原始语言:Breit-Wigner;大陆:布赖特-维格纳;台灣:布萊特-維格納; 当前用字模式下显示为→布赖特-维格纳
- 原始语言:Center-of-mass frame;台灣:質心系;大陆:质心系; 当前用字模式下显示为→质心系
- 原始语言:Central force;台灣:連心力;大陆:有心力; 当前用字模式下显示为→有心力
- 原始语言:Charge-mass ratio;台灣:電荷質量比;大陆:荷质比; 当前用字模式下显示为→荷质比
- 原始语言:Charm;台灣:魅;大陆:粲; 当前用字模式下显示为→粲
- 原始语言:Classical;台灣:古典;大陆:经典; 当前用字模式下显示为→经典
- 原始语言:cold fusion;台灣:冷融合;大陆:冷聚变;香港:冷聚變; 当前用字模式下显示为→冷聚变
- 原始语言:collapse;大陆:坍缩;台灣:塌縮; 当前用字模式下显示为→坍缩
- 原始语言:confinement;台灣:局限;大陆:约束;香港:約束; 当前用字模式下显示为→约束
- 原始语言:confinement fusion;台灣:局限融合;大陆:约束聚变;香港:約束聚變; 当前用字模式下显示为→约束聚变
- 原始语言:criterion;台灣:準則;大陆:判据; 当前用字模式下显示为→判据
- 原始语言:Decoherence;台灣:去相干;大陆:退相干; 当前用字模式下显示为→退相干
- 原始语言:Detect;台灣:偵測;大陆:探测; 当前用字模式下显示为→探测
- 原始语言:Diamagnetism;台灣:反磁性;大陆:抗磁性; 当前用字模式下显示为→抗磁性
- 原始语言:Diffraction;台灣:繞射;大陆:衍射; 当前用字模式下显示为→衍射
- 原始语言:Dimension;台灣:因次;大陆:量纲; 当前用字模式下显示为→量纲
- 原始语言:Double-slit;台灣:雙狹縫;大陆:双缝; 当前用字模式下显示为→双缝
- 原始语言:Dulong-Petit law;台灣:杜隆-泊替定律;大陆:杜隆-珀蒂定律; 当前用字模式下显示为→杜隆-珀蒂定律
- 原始语言:Electron hole;台灣:電洞;大陆:空穴; 当前用字模式下显示为→空穴
- 原始语言:Equation;台灣:方程式;大陆:方程; 当前用字模式下显示为→方程
- 原始语言:Fractal;台灣:碎形;大陆:分形; 当前用字模式下显示为→分形
- 原始语言:Fusion reaction;台灣:融合反應;大陆:聚变反应;香港:聚變反應; 当前用字模式下显示为→聚变反应
- 原始语言:Helium fusion;台灣:氦融合;大陆:氦聚变;香港:氦聚變; 当前用字模式下显示为→氦聚变
- 原始语言:Holography;台灣:全像;大陆:全息; 当前用字模式下显示为→全息
- 原始语言:Hydrogen fusion;台灣:氫融合;大陆:氢聚变;香港:氫聚變; 当前用字模式下显示为→氢聚变
- 原始语言:Informatics;台灣:資訊學;大陆:信息学; 当前用字模式下显示为→信息学
- 原始语言:Information;台灣:資訊;大陆:信息; 当前用字模式下显示为→信息
- 原始语言:Interaction;台灣:交互作用;大陆:相互作用; 当前用字模式下显示为→相互作用
- 原始语言:Ionizing radiation;台灣:游離輻射;大陆:电离辐射; 当前用字模式下显示为→电离辐射
- 原始语言:Legendre transformation;台灣:勒壤得轉換;大陆:勒让德变换; 当前用字模式下显示为→勒让德变换
- 原始语言:Liouville's theorem;台灣:劉維定理;大陆:刘维尔定理; 当前用字模式下显示为→刘维尔定理
- 原始语言:Loop quantum gravity;台灣:迴圈量子重力;大陆:圈量子引力; 当前用字模式下显示为→圈量子引力
- 原始语言:Loop quantum gravity theory;台灣:迴圈量子重力理論;大陆:圈量子引力论; 当前用字模式下显示为→圈量子引力论
- 原始语言:Lyman series;台灣:來曼系;大陆:莱曼系; 当前用字模式下显示为→莱曼系
- 原始语言:Macroscopic;台灣:巨觀;大陆:宏观; 当前用字模式下显示为→宏观
- 原始语言:Magnetic domain;台灣:磁域;大陆:磁畴; 当前用字模式下显示为→磁畴
- 原始语言:Magnetic vector potential;台灣:磁向量位;大陆:磁矢势; 当前用字模式下显示为→磁矢势
- 原始语言:Mean free path;台灣:平均自由徑;大陆:平均自由程; 当前用字模式下显示为→平均自由程
- 原始语言:Mole;大陆:摩尔;台灣:莫耳;香港:摩爾; 当前用字模式下显示为→摩尔
- 原始语言:Net force;繁體:凈力;台灣:淨力;大陆:合力; 当前用字模式下显示为→凈力
- 原始语言:Net external force;繁體:凈外力;台灣:淨外力;大陆:合外力; 当前用字模式下显示为→凈外力
- 原始语言:Nuclear fission;简体:核裂变;繁體:核分裂; 当前用字模式下显示为→核裂变
- 原始语言:Nuclear fusion;简体:核聚变;繁體:核聚變;台灣:核融合; 当前用字模式下显示为→核聚变
- 原始语言:Neutrino;台灣:微中子;大陆:中微子; 当前用字模式下显示为→中微子
- 原始语言:Noise;台灣:雜訊;大陆:噪声; 当前用字模式下显示为→噪声
- 原始语言:Plasma;台灣:電漿;大陆:等离子体;香港:等離子體; 当前用字模式下显示为→等离子体
- 原始语言:Plasma;漿⇒简体:等离子体;漿⇒繁體:漿;漿⇒大陆:等离子体;漿⇒香港:等離子體;漿⇒新加坡:等离子体;漿⇒台灣:漿; 当前用字模式下显示为→等离子体
- 原始语言:Plasma state;台灣:電漿態;大陆:等离子态;香港:等離子態; 当前用字模式下显示为→等离子态
- 原始语言:Positronium;台灣:正子電子偶;大陆:电子偶素; 当前用字模式下显示为→电子偶素
- 原始语言:Potential energy;台灣:位能;大陆:势能; 当前用字模式下显示为→势能
- 原始语言:Probability;台灣:機率;大陆:概率; 当前用字模式下显示为→概率
- 原始语言:Probability;几率⇒简体:几率;几率⇒繁體:機率;几率⇒大陆:几率;几率⇒香港:機率;几率⇒新加坡:几率;几率⇒台灣:機率; 当前用字模式下显示为→几率
- 原始语言:Proper time;台灣:原時;大陆:固有时; 当前用字模式下显示为→固有时
- 原始语言:quark-gluon plasma;大陆:夸克-胶子等离子体;香港:夸克-膠子等離子體;台灣:夸克-膠子漿; 当前用字模式下显示为→夸克-胶子等离子体
- 原始语言:Scalar;台灣:純量;大陆:标量; 当前用字模式下显示为→标量
- 原始语言:Scalar potential;台灣:純量位;大陆:标势; 当前用字模式下显示为→标势
- 原始语言:Singularity;台灣:奇異點;大陆:奇点; 当前用字模式下显示为→奇点
- 原始语言:Shear stress;台灣:切應力;大陆:剪应力; 当前用字模式下显示为→剪应力
- 原始语言:Tesla;台灣:特斯拉;大陆:特斯拉;香港:忒斯拉; 当前用字模式下显示为→特斯拉
- 原始语言:Tunnelling;大陆:隧穿;台灣:穿隧; 当前用字模式下显示为→隧穿
- 原始语言:Turbulence;台灣:亂流;大陆:湍流; 当前用字模式下显示为→湍流
- 原始语言:Unitary;台灣:么正;大陆:幺正; 当前用字模式下显示为→幺正
- 原始语言:Vector;台灣:向量;大陆:矢量; 当前用字模式下显示为→矢量
- 原始语言:Vector potential;台灣:向量位;大陆:矢势; 当前用字模式下显示为→矢势
- 原始语言:Viscosity;台灣:黏性;大陆:粘性; 当前用字模式下显示为→粘性
- 原始语言:Viscoelasticity;台灣:黏彈性;大陆:粘弹性; 当前用字模式下显示为→粘弹性
- 原始语言:Waveguide;台灣:導波;大陆:波导; 当前用字模式下显示为→波导
- 原始语言:Positron;台灣:正子;大陆:正电子; 当前用字模式下显示为→正电子
- 原始语言:Avogadro;台灣:亞佛加厥;大陆:阿伏伽德罗;香港:阿佛加德羅; 当前用字模式下显示为→阿伏伽德罗
- 原始语言:Becquerel;台灣:貝克勒;香港:貝克勒爾;大陆:贝克勒尔; 当前用字模式下显示为→贝克勒尔
- 原始语言:Bernoulli;台灣:白努利;大陆:伯努利; 当前用字模式下显示为→伯努利
- 原始语言:Biot;台灣:必歐;大陆:毕奥; 当前用字模式下显示为→毕奥
- 原始语言:Bohr;台灣:波耳;大陆:玻尔;香港:玻爾; 当前用字模式下显示为→玻尔
- 原始语言:Boltzmann;台灣:波茲曼;大陆:玻尔兹曼; 当前用字模式下显示为→玻尔兹曼
- 原始语言:Bravais;台灣:布拉菲;大陆:布拉维; 当前用字模式下显示为→布拉维
- 原始语言:Brillouin;台灣:布里元;大陆:布里渊; 当前用字模式下显示为→布里渊
- 原始语言:Cherenkov;台灣:契忍可夫;大陆:切连科夫; 当前用字模式下显示为→切连科夫
- 原始语言:D'Alembert;台灣:達朗伯特;大陆:达朗贝尔; 当前用字模式下显示为→达朗贝尔
- 原始语言:Doppler;台灣:都卜勒;大陆:多普勒; 当前用字模式下显示为→多普勒
- 原始语言:Drude;台灣:德汝德;大陆:德鲁德; 当前用字模式下显示为→德鲁德
- 原始语言:Fabry;台灣:法布立;大陆:法布里; 当前用字模式下显示为→法布里
- 原始语言:Fourier;台灣:傅立葉;大陆:傅里叶; 当前用字模式下显示为→傅里叶
- 原始语言:Franck;台灣:法蘭克;大陆:弗兰克; 当前用字模式下显示为→弗兰克
- 原始语言:Gerlach, Walther;台灣:革拉赫;大陆:格拉赫; 当前用字模式下显示为→格拉赫
- 原始语言:Gordon;台灣:戈登;大陆:高登; 当前用字模式下显示为→高登
- 原始语言:Heaviside;台灣:黑維塞;大陆:赫维赛德; 当前用字模式下显示为→赫维赛德
- 原始语言:Hooke;台灣:虎克;大陆:胡克; 当前用字模式下显示为→胡克
- 原始语言:Hubble;台灣:哈柏;大陆:哈勃;香港:哈勃; 当前用字模式下显示为→哈勃
- 原始语言:Ising;台灣:易辛;大陆:伊辛; 当前用字模式下显示为→伊辛
- 原始语言:Jacobi;台灣:亞可比;大陆:雅可比; 当前用字模式下显示为→雅可比
- 原始语言:Kelvin;台灣:克耳文;大陆:开尔文; 当前用字模式下显示为→开尔文
- 原始语言:Kepler;台灣:克卜勒;大陆:开普勒;香港:開普勒; 当前用字模式下显示为→开普勒
- 原始语言:Kirchhoff;台灣:克希荷夫;大陆:基尔霍夫;香港:基爾霍夫; 当前用字模式下显示为→基尔霍夫
- 原始语言:Kruskal;台灣:克魯斯卡;大陆:克鲁斯卡尔; 当前用字模式下显示为→克鲁斯卡尔
- 原始语言:Landau;台灣:蘭道;大陆:朗道; 当前用字模式下显示为→朗道
- 原始语言:Langmuir;台灣:蘭米爾;大陆:朗缪尔; 当前用字模式下显示为→朗缪尔
- 原始语言:Lenz;台灣:冷次;大陆:楞次;香港:楞次; 当前用字模式下显示为→楞次
- 原始语言:Liénard;台灣:黎納;大陆:李纳; 当前用字模式下显示为→李纳
- 原始语言:Lorentz;台灣:勞侖茲;大陆:洛伦兹; 当前用字模式下显示为→洛伦兹
- 原始语言:Lorenz;台灣:勞侖次;大陆:洛伦茨; 当前用字模式下显示为→洛伦茨
- 原始语言:Maxwell;台灣:馬克士威;大陆:麦克斯韦;香港:麥克斯韋; 当前用字模式下显示为→麦克斯韦
- 原始语言:Michelson;台灣:邁克生;大陆:迈克耳孙; 当前用字模式下显示为→迈克耳孙
- 原始语言:Minkowski;台灣:閔考斯基;大陆:闵可夫斯基; 当前用字模式下显示为→闵可夫斯基
- 原始语言:Morley;台灣:莫立;大陆:莫雷; 当前用字模式下显示为→莫雷
- 原始语言:Moseley;台灣:莫斯利;大陆:莫塞莱; 当前用字模式下显示为→莫塞莱
- 原始语言:Olbers;台灣:歐伯斯;大陆:奧伯斯; 当前用字模式下显示为→奧伯斯
- 原始语言:Pauli;台灣:包立;大陆:泡利; 当前用字模式下显示为→泡利
- 原始语言:Penrose;台灣:潘洛斯;大陆:彭罗斯; 当前用字模式下显示为→彭罗斯
- 原始语言:Perot;台灣:培若;大陆:珀罗; 当前用字模式下显示为→珀罗
- 原始语言:Poisson;台灣:帕松;大陆:泊松; 当前用字模式下显示为→泊松
- 原始语言:Poynting;台灣:坡印廷;大陆:坡印亭; 当前用字模式下显示为→坡印亭
- 原始语言:Rayleigh;台灣:瑞立;大陆:瑞利; 当前用字模式下显示为→瑞利
- 原始语言:Reissner;台灣:萊斯納;大陆:雷斯勒; 当前用字模式下显示为→雷斯勒
- 原始语言:Rutherford;台灣:拉塞福;大陆:卢瑟福;香港:盧瑟福; 当前用字模式下显示为→卢瑟福
- 原始语言:Rydberg;台灣:芮得柏;大陆:里德伯; 当前用字模式下显示为→里德伯
- 原始语言:Schrödinger;台灣:薛丁格;大陆:薛定谔;香港:薛定諤; 当前用字模式下显示为→薛定谔
- 原始语言:Snell;台灣:司乃耳;大陆:斯涅尔;香港:斯涅耳; 当前用字模式下显示为→斯涅尔
- 原始语言:Stefan;台灣:斯特凡;大陆:斯特藩; 当前用字模式下显示为→斯特藩
- 原始语言:Stern, Otto;台灣:斯特恩;大陆:施特恩; 当前用字模式下显示为→施特恩
- 原始语言:Joseph Thomson;台灣:湯姆森;大陆:汤姆孙;香港:湯姆生; 当前用字模式下显示为→汤姆孙
- 原始语言:Van de Graaff;台灣:凡德格拉夫;大陆:范德格拉夫; 当前用字模式下显示为→范德格拉夫
- 原始语言:Van der Waals;台灣:凡得瓦;大陆:范德瓦耳斯; 当前用字模式下显示为→范德瓦耳斯
- 原始语言:Verdet;台灣:伐得;大陆:韦尔代; 当前用字模式下显示为→韦尔代
- 原始语言:von Neumann;台灣:馮·諾伊曼;大陆:冯·诺伊曼;香港:馮·紐曼; 当前用字模式下显示为→冯·诺伊曼
- 原始语言:Wien;台灣:維因;大陆:维恩; 当前用字模式下显示为→维恩
- 原始语言:Wiechert;台灣:維謝;大陆:维谢尔; 当前用字模式下显示为→维谢尔
- 原始语言:Wilson;台灣:威爾森;大陆:威耳逊; 当前用字模式下显示为→威耳逊
- 原始语言:Witten;台灣:維騰;大陆:威滕; 当前用字模式下显示为→威滕
- 原始语言:Α,α,alpha;简体:阿尔法;繁體:阿爾法;台灣:阿伐; 当前用字模式下显示为→阿尔法
- 原始语言:Β,β,beta;简体:贝塔;繁體:貝塔;台灣:貝他; 当前用字模式下显示为→贝塔
- 原始语言:Γ,γ,gamma;简体:伽马;繁體:伽瑪; 当前用字模式下显示为→伽马
顯示↓關閉↑字詞轉換说明
字詞轉換是中文维基的一項自動轉換,目的是通過计算机程序自動消除繁简、地区词等不同用字模式的差異,以達到閱讀方便。字詞轉換包括全局轉換和手動轉換,本說明所使用的标题转换和全文转换技術,都屬於手動轉換。
如果您想对我们的字词转换系统提出一些改进建议,或者提交应用面更广的转换(中文维基百科全站乃至MediaWiki软件),或者报告转换系统的错误,请前往Wikipedia:字词转换请求或候选发表您的意见。
拉格朗日力學時常涉及廣義速度。假設一個物理系統的廣義坐標是  ,表示廣義速度為
,表示廣義速度為  。廣義速度定義為廣義坐標隨時間
。廣義速度定義為廣義坐標隨時間 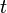 的導數:
的導數:
 。
。
[编辑] 與動能的關係
在三維空間裏,一個質量為 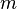 、速度為
、速度為  的粒子的動能是
的粒子的動能是
 。
。
速度是位置 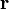 對於時間
對於時間 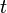 的導數。應用偏微分連鎖律,可以得到
的導數。應用偏微分連鎖律,可以得到
 ;
;
其中, 是第
是第 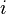 個廣義坐標,
個廣義坐標, 是對應的廣義速度。
是對應的廣義速度。
所以,
 。
。
將方程式展開[1],動能可以分為三個項目表示:
 ;
;
其中,
 ,
, ,
, 。
。
 、
、 、
、 分別為廣義速度
分別為廣義速度  的 0 次、1 次、2 次齊次函數。如果這系統是定常系統,位置不顯性地相依於時間,
的 0 次、1 次、2 次齊次函數。如果這系統是定常系統,位置不顯性地相依於時間, ,則只有
,則只有  不等於零。所以,
不等於零。所以, ,動能是廣義速度的2 次齊次函數。
,動能是廣義速度的2 次齊次函數。