帕塞瓦尔定理
若函数 可积且平方可积,则
可积且平方可积,则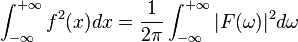 。其中F(ω) 是f(x) 的傅里叶变换。
。其中F(ω) 是f(x) 的傅里叶变换。
更一般化而言,若函数 和
和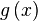 皆平方可积,则
皆平方可积,则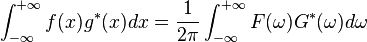 。其中F(ω) 和G(ω) 分别是f(x) 和g(x) 的傅里叶变换, *代表複共軛。
。其中F(ω) 和G(ω) 分别是f(x) 和g(x) 的傅里叶变换, *代表複共軛。
[编辑] 傅里叶变换的不同变种
薛定谔方程二阶随机过程(不含引号)的搜索结果:
搜索结果
-
获得更多知识搜索结果
-
-
薛定谔方程是错误的- nhymj1209的日志- 网易博客
2011年3月25日 – 是将物质波的概念和波动方程相结合建立的二阶偏微分方程。 二、薛定谔方程的错误 ... 从这段话看出,薛定谔方程推导过程中的三点错误: ...
blog.163.com/nhymj1209@126/.../16485550520112250483359/ - 网页快照 -
弱平稳随机过程,weakly stationary stochastic process,在线英语词典 ...
通过数值求解变系数非线性薛定谔方程,发现光纤系统对带有弱“平台”的皮秒光孤子有 .... 在平稳随机过程的数学理论中,过程X(t)的概率分布的矩,尤其是第一、二阶矩一- ...
www.dictall.com/indu/398/3979655BBF0.htm -
309电磁场理论- docin.com豆丁网
2010年4月9日 – 薛定谔方程及一维定态问题薛定谔方程及一维定态问题概论、方势阱、方 ... 随机过程的基本概念 随机过程的概念和有限维分布函数族 随机过程的数字特征 几类重要的随机过程:二阶矩过程、正交增量过程、马尔可夫过程、独立增量过程、 ...
www.docin.com/p-48957821.html - 网页快照