混沌蝴蝶——洛伦兹吸引子
美国气象学家洛伦兹(E.N.Lorenz,不要和提出洛伦兹变换的那位搞混)是混沌理论的奠基者之一。20世纪50年代末到60年代初,他的主要工作目标是从理论上进行长期天气预报。他在使用计算机模拟天气时意外发现,对于天气系统,哪怕初始条件的微小改变也会显著影响运算结果。随后,他在同事工作的基础上化简了自己先前的模型,得到了有3个变量的一阶微分方程组,由它描述的运动中存在一个奇异吸引子,即洛伦兹吸引子。
洛伦兹的工作结果最初在1963年发表,论文题目为Deterministic Nonperiodic Flow,发表在Journal of the Atmospheric Sciences杂志上。如今,这一方程组已成为混沌理论的经典,也是“巴西蝴蝶扇动翅膀在美国引起德克萨斯的飓风”一说的肇始。它的形式看起来很简单:
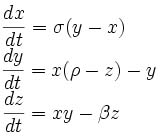
洛伦兹方程组是基于流体力学中的Navier-Stokes方程、热传导方程和连续性方程构建的,属于耗散系统。相空间中,耗散系统的终态都将收缩到吸引子的状态上。但对平庸吸引子来说,无论初值如何,终值只有一个,而奇异吸引子却是无数个点的集合,对初值极端敏感。如洛伦兹当年只是忽略了小数点4位以后的数值,得到的结果就有了相当大的偏差,甚至是完全相反。
在洛仑兹原始的工作中,x表示的是对流的翻动速率,y正比于上流与下流液体温差,z是垂直方向的温度梯度。式中三个参数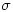 (Prandtl数)、
(Prandtl数)、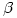 和
和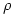 (Rayleigh数)可任取大于0的数值。常用的组合是
(Rayleigh数)可任取大于0的数值。常用的组合是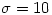 ,
,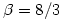 ,而令
,而令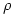 取不同数值。
取不同数值。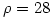 时有混沌现象,奇异吸引子出现,此时系统的演化轨迹如下图所示:
时有混沌现象,奇异吸引子出现,此时系统的演化轨迹如下图所示:
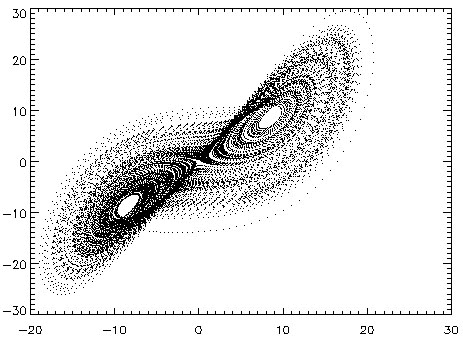
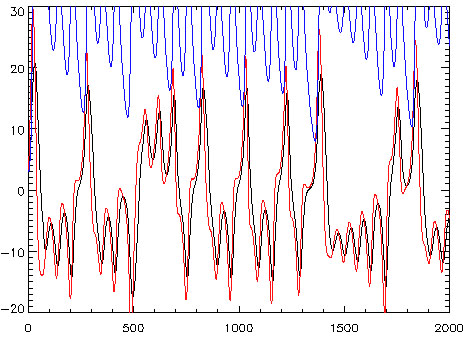
这一图案颇似蝴蝶展翅,所谓混沌理论的“蝴蝶效应”之得名据说也与此吸引子的形状有关。该系统中x、y、z这3个方向数值随时间的演化如下图,其中黑线为x轴变化情况,红线为y轴变化情况,蓝线是z轴变化情况(积分步长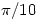 )。
)。
固定另2个参数,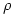 的不同取值则决定了系统的不同性质。下面四图分别为该参数取值1、10、14与99.6时的演化轨迹:
的不同取值则决定了系统的不同性质。下面四图分别为该参数取值1、10、14与99.6时的演化轨迹:
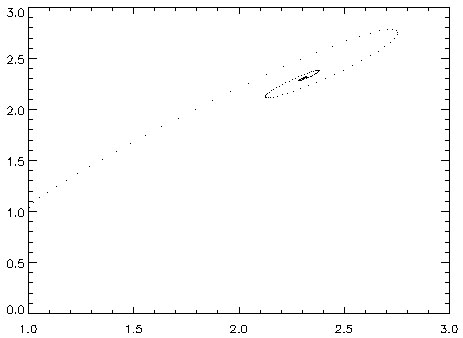
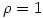
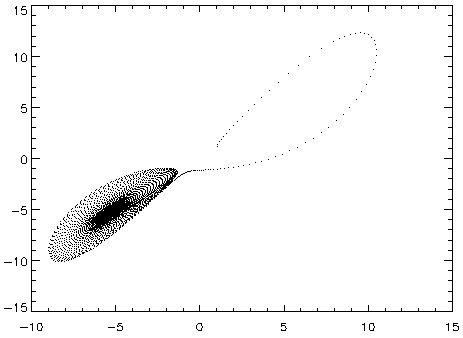
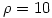
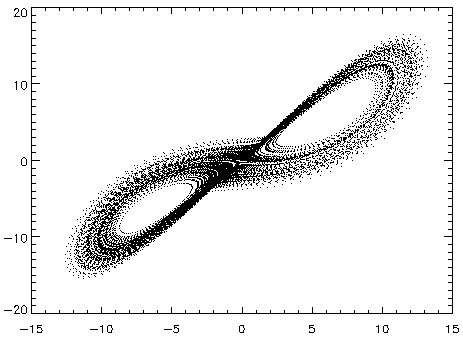
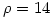
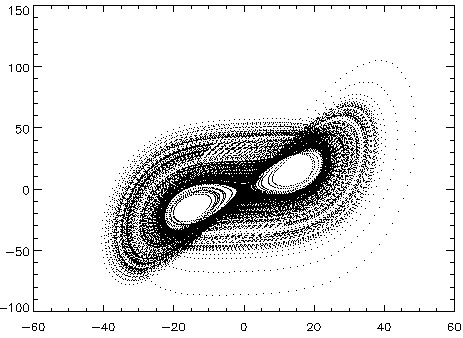
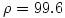
由图中可见,在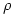 较小(如取1)的情况下,系统是稳定的,演化到两个吸引点中的一个。随着
较小(如取1)的情况下,系统是稳定的,演化到两个吸引点中的一个。随着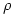 的增加,系统趋于复杂,在
的增加,系统趋于复杂,在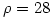 时达到混沌状态。
时达到混沌状态。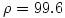 的情况是所谓的圆环结(torus knot)。如果单独看以上三种情况x、y、z坐标的演化,可能会更清楚一些:
的情况是所谓的圆环结(torus knot)。如果单独看以上三种情况x、y、z坐标的演化,可能会更清楚一些:
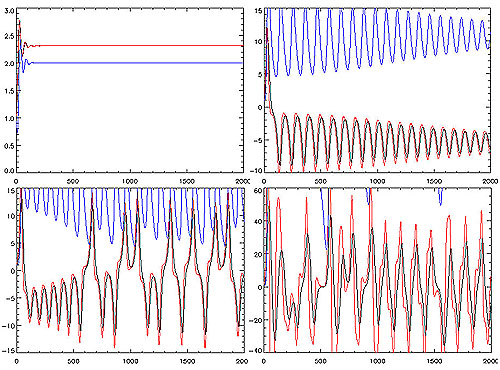
左上: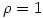 ;右上:
;右上: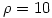 ;左下:
;左下: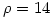 ;右下:
;右下: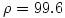
Paul Bourke作出过洛伦兹吸引子的3D图象,并发表在2000年8月31日的Nature杂志上:
