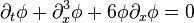孤子波 KdV方程 u[,t]+uu[,x]+u[,xxx]=0

http://www.philosophy.org.cn/Subject_info.aspx?n=20110323164601900122

孤波是色散效应与非线性作用协同互补平衡的结果。最早解出孤波的方程是关于浅水波运动的kdv方程，其基本形式为[5]：u[,t]+uu[,x]+u[,xxx]=0

 

 

其中波函数u表示水波相对静止水面垂直凸起的位移，x为相对波包静止时沿水平方向的空间坐标，t为时间参数。uu[,x]为二次项函数，体现了流体的非线性作用。u[,xxx]是波的三阶空间变化率，体现了流体对波的色散作用。u[,t]体现波的时间变化行为。三者共存于同一方程，构成一种动力学上的量化平衡。受此量化关系的制约，在确定的物理条件下，可得到孤波解。孤波函数u的图形犹如钟状。这种波形恰好可使色散效应和非线性效应相互补偿平衡，确保波包在传播时保持形状不变。任何波形都具有自己确定的频率与振幅分布的单色波群结构，因此满足kdv方程的孤波是由其特定的多元单色波群和谐稳定地构成。

KdV方程是1895年由荷兰数学家科特韦格和德弗里斯共同发现的一种偏微分方程（也有人称之为科特韦格-德弗里斯方程，但一般都习惯直接叫KdV方程）。关于实自变量x 和t 的函数φ所满足的KdV方程形式如下：

KdV方程的解为簇集的孤立子（又称孤子，孤波）。

[编辑] 联系

KdV方程和物理问题有几个联系。 它是弦在Fermi-Pasta-Ulam问题在连续极限下的统治方程。KdV方程也描述弱非线性回复力的浅水波。

KdV方程也可以用逆散射技术求解，譬如那些适用于薛定谔方程的。