李铭 李小文 卷积的意义还得听我说

来源: 于 2011-03-27 20:13:15 [博客] [旧帖] [给我悄悄话] 本文已被阅读：次

[转载]卷积的意义还得听我说

已有 106 次阅读 2011-3-25 01:33 |个人分类:科普|系统分类:教学心得|关键词:卷积

没想到一个卷积引起了不少人的关注，最后还要数学家曹广福出马来做解释。他给出的卷积是 y(s)=∫x(t)h(s-t)dt。 可惜，曹大侠不熟悉信号处理，说起卷积来还是心有余而力不足。我看这个卷积还得由搞实验测量的人来讲才能让人真正明白。
  

我给大家一个更直观的例子。假设我们要测量一群粒子的能谱，也就是不同能量的粒子的个数跟粒子能量的关系I(E)。对于一群能量全都为E'的粒子，在I-E直角坐标系上 I(E) 就应该是在E'处的一个点，在其他地方都为0，如图1所示.

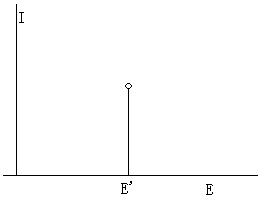   图1
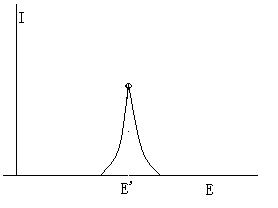  图2.
  但是，我们用来测量粒子能量的任何仪器，总是有误差的。即使测量的是完全相同能量的粒子，仪器测出的能量有时候大一点，有时候小一点，因为测出的能谱不是一个点，而是在这个点两边展开的一条曲线（通常是一条高斯曲线），如图2所示。这条曲线除以粒子总数就是曹大侠说的响应函数X(E)。这条曲线越窄，仪器的能量分辨率就越好。
 
对于一群能量不同的粒子，实验测量出来的能谱是 I(E)。可是，我们不要忘了，这里面的E,  是有误差的。我们想问的是，那个真实的能谱J(E) 是什么样的？于是，卷积就出现了，因为它们的关系是
I(E)=∫X(e) J(E-e)de.
 
这是因为，在能量 E 附近的真实能谱J(E-e) 都对测量出来的E点的能谱I(E)有贡献，贡献的大小由响应函数X(e)决定。现在数学家的任务就是要从测出来的 I(E) 把 J(E)解出来。这是已经完全解决了的问题，有现成的计算机程序。
 
更喜欢离散的形式的人请参考李小文院士的相关博文。
收藏 分享 举报

全部作者的其他最新博文

热门博文导读

相关博文

1 hunagxingbin

发表评论 评论 (1 个评论)

[1]math611  2011-3-26 16:03
卷积是一种相关性，也可以理解成密度投影。这在数学上是很普遍的了，信号处理等都常用。