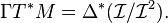星空浩淼 2008-9-30 19:15
[b]三、物理上的实例[/b]
在固体物理中,晶体格点原胞基矢是位置空间中的基向量,与之对偶的基向量是倒格子空间中的基向量,这是波数矢量(即动量矢量)空间中的基向量。另一方面,前面提到过,用d表示偏微分符号,现在微分几何中,通常分别用e_i=d/dx^i和e^j=dx^j来表示基向量和对偶基向量。学过量子力学的知道,d/dx^i与动量算符对应(相差常数因子),如果把e^j=dx^j对应位置空间基向量,这两个例子给人这种感觉:从向量空间到它的对偶空间,例子之一就是从位置空间到动量空间,相应的基向量与对偶基向量可能方向不同,量纲也不同。此时,空间与它的对偶空间有着本质的不同。对于一个物理系统S,它的广义坐标构成位形空间M,M上的余切丛即是系统S的相空间。我们知道,相空间是位形空间(即M)与动量空间的直积空间。这跟这样的事实是相符的:广义动量是M上的协变向量,而余切空间是协变向量空间(余切丛则是位形空间M与余切空间的直积空间)。
在固体物理中,晶体格点原胞基矢是位置空间中的基向量,与之对偶的基向量是倒格子空间中的基向量,这是波数矢量(即动量矢量)空间中的基向量。另一方面,前面提到过,用d表示偏微分符号,现在微分几何中,通常分别用e_i=d/dx^i和e^j=dx^j来表示基向量和对偶基向量。学过量子力学的知道,d/dx^i与动量算符对应(相差常数因子),如果把e^j=dx^j对应位置空间基向量,这两个例子给人这种感觉:从向量空间到它的对偶空间,例子之一就是从位置空间到动量空间,相应的基向量与对偶基向量可能方向不同,量纲也不同。此时,空间与它的对偶空间有着本质的不同。对于一个物理系统S,它的广义坐标构成位形空间M,M上的余切丛即是系统S的相空间。我们知道,相空间是位形空间(即M)与动量空间的直积空间。这跟这样的事实是相符的:广义动量是M上的协变向量,而余切空间是协变向量空间(余切丛则是位形空间M与余切空间的直积空间)。
 是 M 上光滑函数
是 M 上光滑函数 由高阶项为 0 的等价类组成。余切丛是这个层
由高阶项为 0 的等价类组成。余切丛是这个层