环量是流体的速度沿着一条闭曲线的路径积分，环量的量纲是长度的平方除以时间, 。而只给出矢量场A的旋度，无法确定A，只有通过规定A

来源: marketreflections 于 2011-03-02 17:55:42 [博客] [旧帖] [给我悄悄话] 本文已被阅读：次

环量

维基百科，自由的百科全书

跳转到：导航, 搜索

环量是流体的速度沿着一条闭曲线的路径积分，通常用 $Γ$ 来表示。如果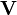 $\mathbf{V}$ 是流体的速度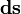， $\mathbf{ds}$ 是沿着闭曲线 $C$ 的单位向量，那么：

$\Gamma=\oint_{C}\mathbf{V}\cdot\mathbf{ds}$

环量的量纲是长度的平方除以时间。

[编辑] 库塔-儒可夫斯基定理

物体在无粘流动场中单位长度所受到的升力，可以表示为环量（ $Γ$ ）、流体的密度（ $ρ$ ）和物体相对于自由流的速度（ $V$ ）的乘积。因此：

l = - ρ V Γ

在计算流体力学中，环量经常作为中间变量，用来计算翼型或其它物体所受到的力。

通过斯托克斯定理，环量与涡度之间有以下的关系：

$\Gamma=\oint_{C}\mathbf{V}\cdot\mathbf{ds}=\int\!\!\!\int_S(\nabla\times\mathbf{V})\cdot\mathbf{dS}$

但仅当积分路径是一个边界，而不仅仅是一个闭曲线时，这个等式才成立。