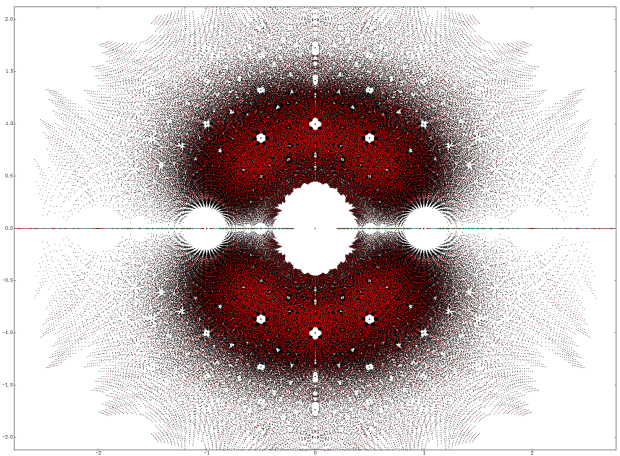
高次多项式集中在人魔交接界,信息模糊时,波动大 Dan Christensen发现,把所有次数不超过5的、系数在-4到4范围内的整系数多项式的所有根描绘在同一个复平面上,你会看到一个异常壮观的画面。图中的每个灰色点代表某个二次多项式的一个根,蓝色点代表三次多项式的根,红色代表四次多项式的根,黑色代表五次多项式的根。水平线代表实轴,0和±1的地方有很明显的空洞;竖直方向是虚轴,每个单位根处也都有明显可辨的空洞。 §9 有理系数多项式 作为因式分解定理的一个特殊情形,有每个次数≥1的有理系数多项式都能分解成不可约的有理系数多项式的乘积.但是对于任何一个给定的多项式,要具体地作出它的分解式却是一个很复杂的问题,即使要判别一个有理系数多项式是否可约也不是一个容易解决的问题,这一点是有理数域与复数域、实数域不同的.在这一节主要是指出有理系数多项式的两个重要事实:第一,有理系数多项式的因式分解的问题,可以归结为整(数)系数多项式的因式分解问题,并进而解决求有理系数多项式的有理根的问题.第二,在有理系数多项式环中有任意次数的不可约多项式. 一、有理系数多项式的有理根 设 是一个有理系数多项式.选取适当的整数 乘 ,总可以使 是一个整系数多项式.如果 的各项系数有公因子,就可以提出来,得到 , 也就是 其中 是整系数多项式,且各项系数没有异于±1的公因子. 如果一个非零的整系数多项式 的系数 没有异于±1的公因子,也就是说它们是互素的,它就称为一个本原多项式.上面的分析表明,任何一个非零的有理系数多项式 都可以表示成一个有理数 与一个本原多项式 的乘积,即 . 可以证明,这种表示法除了差一个正负号是唯一的.亦即,如果 , 其中 都是本原多项式,那么必有 因为 与 只差一个常数倍,所以 的因式分解问题,可以归结为本原多项式 的因式分解问题.下面进一步指出,一个本原多项式能否分解成两个次数较低的有理系数多项式的乘积与它能否分解成两个次数较低的整系数多项式的乘积的问题是一致的. 定理10(Gauss 引理) 两个本原多项式的乘积还是本原多项式. 定理11 如果一非零的整系数多项式能够分解成两个次数较低的有理系数多项式的乘积,那么它一定可以分解两个次数较低的整系数多项式的乘积. 以上定理把有理系数多项式在有理数域上是否可约的问题归结到整系数多项式能否分解成次数较低的整系数多项式的乘积的问题. 推论 设 , 是整系数多项式,且 是本原多项式,如果 ,其中 是有理系数多项式,那么 一定是整系数多项式. 这个推论提供了一个求整系数多项式的全部有理根的方法. 定理12 设 是一个整系数多项式.而 是它的一个有理根,其中 互素,那么 (1) ;特别如果 的首项系数 ,那么 的有理根都是整根,而且是 的因子. (2) 其中 是一个整系数多项式. 给了一个整系数多项式 ,设它的最高次项系数的因数是 ,常数项的因数是 那么根据定理12,欲求 的有理根,只需对有限个有理数 用综合除法来进行试验. 当有理数 的个数很多时,对它们逐个进行试验还是比较麻烦的.下面的讨论能够简化计算. 首先,1和-1永远在有理数 中出现,而计算 与 并不困难.另一方面,若有理数 是 的根,那么由定理12, 而 也是一个整系数多项式.因此商 都应该是整数.这样只需对那些使商 都是整数的 来进行试验.(我们可以假定 与 都不等于零.否则可以用 或 除 而考虑所得的商.) 例1 求多项式 的有理根. 例2 证明 在有理数域上不可约. 二、有理数域上多项式的可约性 定理13 (艾森斯坦(Eisenstein)判别法) 设 是一个整系数多项式.若有一个素数 ,使得 1. ; 2. ; 3. . 则多项式 在有理数域上不可约. 由艾森斯坦判断法得到: 有理数域上存在任意次的不可约多项式.例如 .,其中 是任意正整数. 艾森斯坦判别法的条件只是一个充分条件. 有时对于某一个多项式 ,艾森斯坦判断法不能直接应用,但把 适当变形后,就可以应用这个判断法. 例3 设 是一个素数,多项式 叫做一个分圆多项式,证明 在 中不可约. 证明:令 ,则由于 , , 令 ,于是 , 由艾森斯坦判断法, 在有理数域上不可约, 也在有理数域上不可约.