泊松括号
维基百科,自由的百科全书
在數學及经典力學中,泊松括號是哈密顿力學中重要的運算,在哈密頓表述的動力系統中時間演化的定義起着中心角色。在更一般的情形,泊松括号用来定义一个泊松代数,而泊松流形是一个特例。它们都是以西莫恩·德尼·泊松命名的。
目录[隐藏] |
[编辑] 正則坐標
在相空间里,用正則坐標  ,两个函数
,两个函数 的泊松括號具有如下形式:
的泊松括號具有如下形式:
[编辑] 运动方程
哈密顿-雅可比运动方程有一个使用泊松括号的等价表示。这可最直接地用坐标系表示。假设 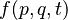 是流形上一个函数,则我们有
是流形上一个函数,则我们有
然后,取 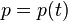 与
与 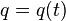 为哈密顿-雅可比方程
为哈密顿-雅可比方程 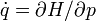 与
与  的解,我们有
的解,我们有
从而,辛流形上一个函数 f 的演化可用辛同胚单参数族给出,以时间 t 为参数。丢掉坐标系,我们有
算子  称为刘维尔算子。
称为刘维尔算子。
[编辑] 运动常数
一个可积动力系统可能有能量以外的运动常数。这样的运动常数在泊松括号下将与哈密顿量交换。假设某个函数  是一个运动常数。这意味着如果
是一个运动常数。这意味着如果  是哈密顿运动方程的一条轨迹或解,则沿着轨迹有
是哈密顿运动方程的一条轨迹或解,则沿着轨迹有  。这样我们有
。这样我们有
这里中间步骤利用运动方程得到。这个方程称为刘维尔方程。刘维尔定理描述了如上给出的一个测度(或相空间上分布函数)的时间演化。
为了使一个哈密顿系统完全可积,所有的运动常数必须互相对合。


![\{f,g\} = \sum_{i=1}^{N} \left[ \frac{\partial f}{\partial q^{i}} \frac{\partial g}{\partial p_{i}} - \frac{\partial f}{\partial p_{i}} \frac{\partial g}{\partial q^{i}} \right] .](http://upload.wikimedia.org/wikipedia/zh/math/0/e/1/0e1555bd009b51b3e98fabbf5524c85c.png)

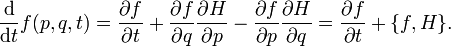


 选择“Disable on www.wenxuecity.com”
选择“Disable on www.wenxuecity.com”
 选择“don't run on pages on this domain”
选择“don't run on pages on this domain”

