转载]泛函分析- 王伟华的博文- 科学网
算符 (物理學)
| 物理算符 |
|---|
| 位置算符 |
| 動量算符 |
| 角動量算符 |
| 哈密頓算符 |
| 時間演化算符 |
| 階梯算符 |
| 創生及湮滅算符 |
| 自旋算符 |
| [編輯] |
在物理學裏,算符,又稱算子,作用於物理系統的物理態 (physical state),使得物理系統從一個物理態變換為另外一個物理態。通過這變換,我們時常會得到一些關於這兩個物理態的資料。
目录[隐藏] |
[编辑] 在經典力學裏的算符
思考一個經典力學系統,哈密頓量  是參數為廣義坐標
是參數為廣義坐標 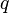 與其共軛動量
與其共軛動量 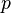 的函數。假設在某種群
的函數。假設在某種群 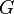 的變換運算下,哈密頓量是個不變量;也就是說,假設
的變換運算下,哈密頓量是個不變量;也就是說,假設 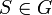 ,則
,則 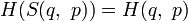 。所有
。所有 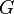 的元素都是物理算符,將物理態映射至另外一個物理態,同時保持哈密頓量恆定。
的元素都是物理算符,將物理態映射至另外一個物理態,同時保持哈密頓量恆定。
再舉一個關於平移於空間的簡單例子。設定  為一個平移算符(translation operator),一個對於平移保持不變的物理系統,在
為一個平移算符(translation operator),一個對於平移保持不變的物理系統,在  變換下,其哈密頓量保持不變。
變換下,其哈密頓量保持不變。
假設物理系統可以由一個函數 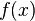 描述,像在經典場理論裏,則平移算符一般表達為
描述,像在經典場理論裏,則平移算符一般表達為
 。
。
請注意,在括弧內的變換是坐標的變換的逆反。
[编辑] 生成子概念
思考一個無窮小的變換,其算符的形式為
 ;
;
其中,  是單位算符,算符的群的單位元,
是單位算符,算符的群的單位元, 是無窮小值參數,
是無窮小值參數, 稱為群的生成元,專門用來設定這變換。
稱為群的生成元,專門用來設定這變換。
讓我們導引出一維平移於空間的生成元。將平移算符  作用於函數
作用於函數 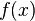 :
:
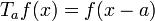 。
。
假設  為無窮小值,則
為無窮小值,則
 。
。
這方程式可以重寫為
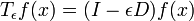 ;
;
其中, 是平移群的生成元,正好也是導數算符。所以,平移群的生成元是導數算符。
是平移群的生成元,正好也是導數算符。所以,平移群的生成元是導數算符。
[编辑] 指數映射
在正常情況下,通過指數映射,可以從生成元得到整個群。對於平移於空間這案例,重複地做  次無窮小平移變換
次無窮小平移變換 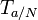 ,來代替一個有限值為
,來代替一個有限值為  的平移變換
的平移變換  :
:
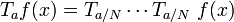 ;
;
現在,讓  變的無窮大,則每一個因子可以被認為無窮小的:
變的無窮大,則每一個因子可以被認為無窮小的:
 。
。
這極限可以重寫為一個指數函數:
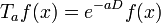 。
。
為了要進一步信服這表達式的正確性,將指數展開為一個冪級數:
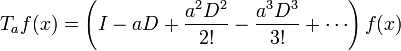 。
。
右手邊可以重寫為
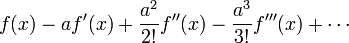 。
。
這正是 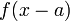 的泰勒級數,也是原本表達式
的泰勒級數,也是原本表達式  的值。
的值。
[编辑] 在量子力學裏的角色
在量子力學裏,算符充分地發揮了它奇妙的功能。量子力學的數學描述建立於算符的概念。
在量子力學裏,一個量子系統的量子態可以用態向量來抽象地表達;而這態向量是某種向量空間(一個希爾伯特空間)的單位範數向量。在這向量空間內,時間演化算符促使了量子態隨著時間的演化。因為物體的量子態的範數應該保持不變,時間演化算符必須是么正算符。任何其他的對稱性運算,從一個物理態映射至另外一個物理態,應該遵守此限制。
物理實驗中可以觀測到的物理量稱為可觀測量。對應於每一個可觀測量,都有一個厄米算符。實驗觀測到的數值是這算符的本徵值。每個本徵值的機率,跟量子態在那本徵值子空間的投影有關。
[编辑] 量子算符
一個量子系統的量子態,受到量子算符 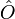 的作用,會變換為另外一個量子態,以方程式表達,
的作用,會變換為另外一個量子態,以方程式表達,
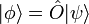 ;
;
其中, 是代表原本量子態的態向量,而
是代表原本量子態的態向量,而  則是代表新量子態的態向量。
則是代表新量子態的態向量。
量子算符的概念比較抽象。它能夠更加簡易的描述量子系統。每一個量子算符,在位置空間,有一個對應的代數算符[1],標記為 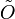 。代數算符的作用對象是波函數。代數算符是對於波函數的一些運算指示,以方程式表達,
。代數算符的作用對象是波函數。代數算符是對於波函數的一些運算指示,以方程式表達,
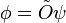 ;
;
其中,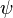 是原本態向量的波函數,而
是原本態向量的波函數,而 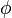 則是新的波函數。
則是新的波函數。
例如,在位置空間裏,計算位置的位置算符  ,其對應的代數算符
,其對應的代數算符  的形式就是乘以
的形式就是乘以  :
:
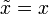 。
。
計算動量的動量算符  ,其對應的代數算符
,其對應的代數算符  的形式就是取對於
的形式就是取對於  的偏微分,然後再乘以
的偏微分,然後再乘以  :
:
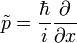 。
。
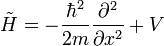 。
。
一般而言,量子算符與代數算符都會用在量子力學裏。當我們將算符的這兩種概念融會貫通後,兩者的區分並不是那麼的重要。
[编辑] 期望值
[编辑] 位置的期望值
思考位置的|期望值,
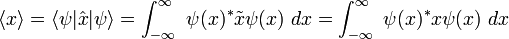 。
。
對於任意波函數 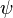 ,這方程式都成立。所以,位置算符
,這方程式都成立。所以,位置算符  所對應的代數算符
所對應的代數算符 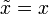 的確可以用來計算位置的期望值。
的確可以用來計算位置的期望值。
[编辑] 動量的期望值
思考位置的期望值隨時間的導數, 用積分方程式來表達,
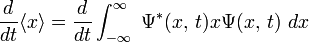 。
。
取微分於積分號下,
 。
。
由於  只是一個位置的統計參數,不相依於時間,
只是一個位置的統計參數,不相依於時間,
 。(1)
。(1)
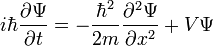 ;
;
其中, 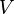 是位勢。
是位勢。
其共軛複數為
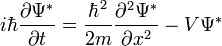 。
。
代入方程式 (1):
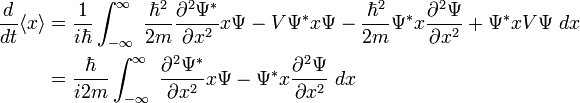 。
。
使用分部積分法,
 ,(2)
,(2)
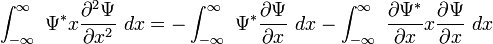 。(3)
。(3)
方程式 (2) 與 (3) 的減差是
 。
。
所以,
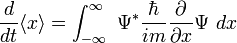 。
。
在經典力學裏,動量是質量乘以位置隨時間的全導數:
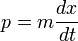 。
。
在量子力學裏,由於粒子的位置不是明確的,而是機率性的。所以,我們猜想這句話是以期望值的方式來實現[2]:
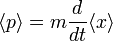 。
。
所以,
 。
。
對於任意波函數 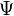 ,這方程式都成立。所以,動量算符
,這方程式都成立。所以,動量算符  ,所對應的代數算符
,所對應的代數算符 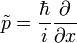 ,的確可以用來計算動量的期望值。
,的確可以用來計算動量的期望值。
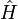 ,其對應的代數算符
,其對應的代數算符 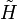 的形式就是
的形式就是 选择“Disable on www.wenxuecity.com”
选择“Disable on www.wenxuecity.com”
 选择“don't run on pages on this domain”
选择“don't run on pages on this domain”

