接着上面两篇博文进行久违的科普, 为科学网大学做点贡献.
YC说,写好的科普就要从什么是相因子这样最基本的概念讲起。这还真是有点为难大呆,这不是我的强项。当然,既然做科普了,还是尽量做好吧。所谓的相因子,就是在波函数中的一个指数因子ei 。实际上,就是一个复数。再向下问:什么是复数?我就要从自然数、实数、虚数。。。一路说下来,得累个半死:-)。简单地做个形象的比方,因子ei
。实际上,就是一个复数。再向下问:什么是复数?我就要从自然数、实数、虚数。。。一路说下来,得累个半死:-)。简单地做个形象的比方,因子ei 可以写成实数和虚数两部分之和cos
可以写成实数和虚数两部分之和cos +isin
+isin ,可以看成以实数为横坐标轴,虚数为纵坐标轴的二维平面内的一个旋转,旋转角度为
,可以看成以实数为横坐标轴,虚数为纵坐标轴的二维平面内的一个旋转,旋转角度为 。
。
 。实际上,就是一个复数。再向下问:什么是复数?我就要从自然数、实数、虚数。。。一路说下来,得累个半死:-)。简单地做个形象的比方,因子ei
。实际上,就是一个复数。再向下问:什么是复数?我就要从自然数、实数、虚数。。。一路说下来,得累个半死:-)。简单地做个形象的比方,因子ei 可以写成实数和虚数两部分之和cos
可以写成实数和虚数两部分之和cos +isin
+isin ,可以看成以实数为横坐标轴,虚数为纵坐标轴的二维平面内的一个旋转,旋转角度为
,可以看成以实数为横坐标轴,虚数为纵坐标轴的二维平面内的一个旋转,旋转角度为 。
。有人说,增加一个公式减少一半的读者。所以,写好的科普文章要尽量不要写公式。甚至于,要想发表Nature/Sciences的文章也要尽量少写公式,否则编辑那一关都通不过。遗憾的是,科学研究的规律并不是公式越少越好,在一些关键的时候还是公式说了算。因为一个公式可以顶一百句无谓的解释。所以,本期博文尽管是科普,还是要夹带一些公式的。如果您看不懂公式,没有关系,直接跳过公式,看文字即可。大呆看文献常常这么干:-)
Berry相效应:已知满足薛定谔方程
 的波函数为|
的波函数为| (t)>。在量子系统通常存在一个动力学相exp(iEt/h)。(本文h加杠) 在某个时刻,我们有本征值方程
(t)>。在量子系统通常存在一个动力学相exp(iEt/h)。(本文h加杠) 在某个时刻,我们有本征值方程 。Berry发现,一个沿参数空间的回路C绝热变化的哈密顿量H(t) 的一个非简并量子态|
。Berry发现,一个沿参数空间的回路C绝热变化的哈密顿量H(t) 的一个非简并量子态| (t)>,要求除了正常的动力学相
(t)>,要求除了正常的动力学相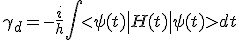 外(它是
外(它是 t的普遍形式),还有一个与回路的几何相关的相。包括几何相关相的波函数|
t的普遍形式),还有一个与回路的几何相关的相。包括几何相关相的波函数| (t)>=exp[
(t)>=exp[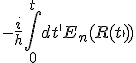 ] exp(
] exp(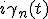 )|n(R (t))>也满足上述薛定谔方程。这个满足薛定谔方程的波函数|
)|n(R (t))>也满足上述薛定谔方程。这个满足薛定谔方程的波函数| (t)>在环绕C后产生的总相变化为|
(t)>在环绕C后产生的总相变化为| (T)>=exp(
(T)>=exp(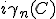 )exp[
)exp[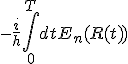 ] )|
] )| (0)>,其中几何相为
(0)>,其中几何相为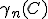 =i
=i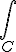
 |
|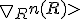 dR。即Berry相(这里的积分为回路积分, 科学网的公式编辑器实在是令人头痛)。
dR。即Berry相(这里的积分为回路积分, 科学网的公式编辑器实在是令人头痛)。

 的波函数为|
的波函数为| (t)>。在量子系统通常存在一个动力学相exp(iEt/h)。(本文h加杠) 在某个时刻,我们有本征值方程
(t)>。在量子系统通常存在一个动力学相exp(iEt/h)。(本文h加杠) 在某个时刻,我们有本征值方程 。Berry发现,一个沿参数空间的回路C绝热变化的哈密顿量H(t) 的一个非简并量子态|
。Berry发现,一个沿参数空间的回路C绝热变化的哈密顿量H(t) 的一个非简并量子态| (t)>,要求除了正常的动力学相
(t)>,要求除了正常的动力学相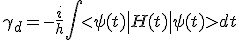 外(它是
外(它是 t的普遍形式),还有一个与回路的几何相关的相。包括几何相关相的波函数|
t的普遍形式),还有一个与回路的几何相关的相。包括几何相关相的波函数| (t)>=exp[
(t)>=exp[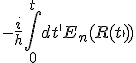 ] exp(
] exp(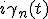 )|n(R (t))>也满足上述薛定谔方程。这个满足薛定谔方程的波函数|
)|n(R (t))>也满足上述薛定谔方程。这个满足薛定谔方程的波函数| (t)>在环绕C后产生的总相变化为|
(t)>在环绕C后产生的总相变化为| (T)>=exp(
(T)>=exp(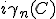 )exp[
)exp[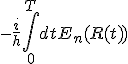 ] )|
] )|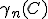 =i
=i |
|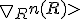 dR。即Berry相(这里的积分为回路积分, 科学网的公式编辑器实在是令人头痛)。
dR。即Berry相(这里的积分为回路积分, 科学网的公式编辑器实在是令人头痛)。Berry实际上是发现, 薛定谔方程的解是不唯一的。在原来大家都知道的动力学相解之外, 或者说, 更深一层次, 还存在一个几何相的贡献。
Berry相是一种拓扑相效应,在量子和经典层次都有表现。在系统缓慢地沿一个回路运动时,除了有内部时钟记录时间的流逝产生动力学相之外,系统还用深层次的几何方式记录其历史,甚至是隐藏在系统从未访问过的参数空间区域的相函数。Simon解释,这个几何相可以被视为在一个适合于量子系统的弯曲空间的平行传递的结果,可以用和乐(holonomy)表示,相可以从Hermitain线丛的曲率(第一陈类)产生。这里的陈即著名数学家陈省身。
简单地解释一下与Berry相相关的平行传递: 打个比方,一个人带着一支箭在地球上赤道上A点向北极出发,箭头开始时指向正北。沿某个经线向北走,行走过程中一直保持箭头的指向在局域环境下不变。到达北极后再沿另外一个经线向南走,到达赤道上B点,然后在沿纬线向西走回到A点。这时候,箭头的指向与出发时的指向成一个角度,可以用这个角度来表示相位的变化(见图)。这个相位的变化与行走在球面上相关,所以,称之为几何相。

实际上,Berry相的存在意味着,即使我们可以(违背相对论原理)乘坐时空隧道回到过去的自己,由于在时空中经历了这个返回的过程,也使我们无法变回过去的自己。即使我们站到了过去的某个时空点上,我已经不是过去的我了。
Berry同时证明了Aharonov-Bohm效应也是一个几何相。Berry相有几种更普遍的形式:1)Wilczek和Zee去除了非简并的限制将一个简并的流形的演变和相与一个非阿贝尔规范联系在一起。2)Berry以及Jackiw等人去除了绝热的限制,发展了一个演变的(非周期)态和相的渐近展开。3)Aharonov和Anandan将问题变成量子系统的自身的回路,而不是哈密顿量在参数空间的回路。这样,无论哈密顿量是否是循环的或绝热的,几何相仅依赖于系统自身的循环演变。这将几何相与无需绝热回路的Aharonov-Bohm效应联系在一起。实际上,在动量空间的Berry相效应是在坐标空间Aharonov-Bohm效应的关联。
Berry相效应与Aharonov-Bohm效应的关联还不仅仅在于此。另外一个关联就是,发现者的单位是同一所学校Bristol大学。英国的大学的自由探索的学术氛围,研究传统的坚持和传承,是值得我们研究和学习的。写科普文章总要写一些有趣的事情。不过难点也就在这个有趣上。本期博文就说点Berry的八卦:在去参加国际会议之前,大呆从网上下载了Berry一些资料,当然也包括他的照片。发现他的脸色红得很,有点不太正常。等到会议现场见到本人,也觉得有点红得不太正常。什么原因?大呆呆想了一阵,发现Berry有一个爱好,喜爱穿红衬衫。所以,常常印得满脸红光四射的样子。如若不信,有照片为证:-)
下一回将介绍另外一个相因子效应,意义重大的并已经用重要应用的Josephson效应。