若的 核是非平凡的,則格林函數不只一個。不過,實際上因著對稱性、邊界條件或其他的因素,可以找到唯一的格林函數。一般來說,格林函數
所有跟帖:
•
格林函數01 电势和电荷是共轭量,两个中只能确定一个
-marketreflections-
♂
![]()
![]() (29871 bytes)
()
06/25/2011 postreply
21:22:54
(29871 bytes)
()
06/25/2011 postreply
21:22:54
•
格林函数01 物理意义为在 处的一个单位电荷在空间 处所激发的电势
-marketreflections-
♂
![]()
![]() (27540 bytes)
()
06/26/2011 postreply
06:47:06
(27540 bytes)
()
06/26/2011 postreply
06:47:06
 ,伴隨著一個在
,伴隨著一個在
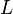 ,為以下方程式的解
,為以下方程式的解
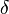 為
為