在局部坐标系中定义的"局部"物体，通过指定局部坐标系在世界坐标系中的方位，利用几何变换，就可以将"局部"定义的物体变换到世界坐标

http://www.cnblogs.com/6666/archive/2009/9/24.html

1、用多维数列表示低维空间坐标,加深理解齐次坐标表示法。

    齐次坐标表示法可以方便地运算，同时形状不变。[x,y,z,0]表示一个无穷的点。

 

在局部坐标系中定义的"局部"物体，通过指定局部坐标系在世界坐标系中的方位，利用几何变换，就可以将"局部"定义的物体变换到世界坐标系内，使之升级成为世界坐标系中的物体

 

为什么会有左手坐标系与右手坐标系之分？
      在3D空间(没错！就是3D)中，所有2D坐标系是等价的（就是通过一系列的仿射变换，可以互相转换）
      而3D坐标系不是等价的，通过仿射变换，是无法将左手坐标系转换到右手坐标系；也就是说，物体坐标系用的就是左手坐标系，世界坐标系用的是右手 坐标系，那么物体可能就是不会是我们所希望的样子了，可能是倒立的，也可能是背对着我们的，所以我们要区分左手坐标系与右手坐标系。也许在4D空间，左右 手坐标系就可以互相变换了吧。

Silverlight和云计算合作开发一个项目？

1我打算建立一个自己的网站，纯粹是学习最近的新技术。

客户端：用Silverlight作为客户端 。
数据库：用云计算。
服务器端：用ASP.NET MVC作为服务器端。

第一种想法：全部使用Silverlight，网页嵌入到Silverlight中，不用JavaScript技术，也就是开发Silverlight全站。

第二种想法：部分使用Silverlight技术，将Silverlight技术嵌入到网页中，利用JavaScript和Silverlight同时开发。

 

第二种开发容易些，因为可以利用别人做好的很多模块。

第一种方法一切都要靠自己去开发新的模块，但是比较有意思。

 

大家认为呢！

还有我的云计算知识和ASP.NET MVC 架构 还在学习阶段，一次都没用过，希望大家多多帮助。

posted @ 2009-09-24 19:06 王书奎(网名:无忌) 阅读(185) | 评论(2) | 编辑

 

 

Silverlight计算机图形学概念理解-笛卡尔坐标系

现在面试Silverlight的时候，很多都提到了计算机图形学，我当时一点都不会，虽然面试通过，但是还是想去接触一下计算机图形学。
而计算机图形学是一个很复杂的东西，涉及到高等数学的所有知识：微积分，线性代数，立体几何，概率，而且还涉及到物理方面的一些知识。所以比较复杂，其实我们没必要搞的很复杂，但是稍微理解一下，比如：矢量，颜色，光线等，然后把关于坐标计算的那一块学好就可以了。

所谓笛卡尔坐标系 就是正交线性坐标系 他是一个数学概念, 并没有规定如何去画.

就传统教学而言, 二维笛卡尔坐标系往往被绘制成y向上,x向右, 两轴成直角. 这源自古老的建筑学以及三角测绘法。建筑的高度应该是从地面向上算的。你可以想象若是y从房顶向下（于是坐标系随着房高浮动），或者从地面向下（于是地窖坐标是正数，而主体会是负数）会是多么不自然。
但这并不是必须的。俯视图如何定向都没有关系；事实上,连轴是不是叫做x, y都没有规定, 又谈何xy的正反向呢?         
当我们看看初等物理时,就会发现我们需要先指定参考系;又常常在笛卡尔坐标系下绘制 电压-时间,        路程-加速度 图像.       
在空间几何中, 你就会看到任意方向绘制的3维笛卡尔坐标系. 其中x,y, z任意两轴可以任意指定方向,不过一般满足Z的方向为 X <B>x </B>Y <B>[注2]</B>        .当然这是为了叉乘运算的方便.

至于计算机为什么采用y向下的坐标系呢? 这同样是有传统的: CRT显示器的扫描方式是从上到下按行扫描<B>[注3]</B>, 第一行在最上面, 往下依次数.        同样,为了便于显示,显卡中的渲染缓存也是这样布置画面的,大部分位图格式譬如bmp, jpg亦如此。他的另一个好处是: 与我们的阅读习惯相同。我们知道,早期的电脑主要用于处理文本, 而文本无论在显示器上还是在存储器内, 都是从上到下逐行排布的。你同样可以想象，上面这几处若是把y轴反过来朝上会造成多大麻烦，所以图形学传统上采用这种y轴向下的坐标系              

事实上只要你从头到尾都使用这个坐标系, 他没什么不合适的. 去除你心中根深蒂固的老坐标系把( 事实上本身就不存在... )               
, Silverlight的所有概念都是以y向下的坐标系为基础的. 它和Math对象配合非常完美
当然, y轴向上还是向下是有区别的, 它意味着x运算(或者说潜在的z轴)反向了,于是所谓顺时针和逆时针的意义变得不同:你用计算平面正反向, 或者进行矢量运算判断上下的时候要注意这一点.

posted @ 2009-09-24 18:33 王书奎(网名:无忌) 阅读(296) | 评论(0) | 编辑

 

 

Silverlight 计算机图形学3 三维空间坐标

第一：奇次坐标

为什么要引入齐次坐标呢？这主要是由于以下两方面的原因：
    首先，在物理学中, 矢量用于表示力和速度等物理量， 通常用具有长度和方向的线段来表示，如图4.1表示。我们往往用数学符号 表示一个矢量。它与空间位置无关。对于三维空间中位于(x, y, z)处的一个点P, 如果我们用一个列矩阵 来表示它, 这与矢量的表示会引起混淆。
    其次，在二维或三维空间中，矩阵的乘积，例如Q＝TP，只能表示旋转、比例和剪切等等变换，而不能表示平移变换。



   
例如, 在图4.2中，点P绕坐标原点旋转θ角后到达P′，其坐标可以用下式计算：
（4－1－1）
　　
其中
　　
。
    对于比例、反射和剪切等变换，我们都可以得到类似（4－1－1）式的矩阵表达式。但是，如果我们将物体沿直线路径从一个坐标位置平移到另一个坐标位置，即通过给原始坐标位置（x,y,z）加上平移距离t_x、t_y和t_z后，使它移到新的位置(x′, y′, z′)。令P＝[x, y, z]^T, P_t=[t_x , t_y , t_z]^T, P′＝[x′, y′, z′]^T, 则
。 （4－1－2）
上式的右边就不能象（4－1－1）式的右边那样写成两个矩阵相乘的形式。
    为了避免这些困难，我们用4维列矩阵来表示三维空间中的点和矢量。假定用（e₁, e₂, e₃, P₀）指定三维空间坐标系的框架，其中，e₁, e₂和e₃是坐标轴矢量，P₀是坐标原点。则空间中的任何一个点P都可以在该坐标系框架下唯一地写成
。

我们可以用矩阵乘积的形式把上式改写成
。
严格地讲，上式并不是一个点积或内积，因为其矩阵的元素是不同的。上式右边的4维行矩阵就是P点在给定的坐标系框架下的齐次坐标表示。或者等价地说，P点的齐次坐标可以用4维列矩阵表示为
。
在同一个坐标系框架下，任何矢量V都可以写成

，
于是，V能够用列矩阵表示为 。
应当指出，这个式子几何上有不同的解释，我们在后面还会介绍。


 
仿射变换


仿射变换是计算机图形学中最常用的变换。下列形式的坐标变换称为三维仿射变换：
左（4－2－1）
即：Q的坐标是P的坐标的线性组合。它可以用齐次坐标来表示：
左（4－2－2）
    仿射变换将矢量变换成为矢量。如上一节所述，如果空间矢量V的坐标是V_x, V_y和V_z，它的坐标框架表示（即齐次坐标表示）是一个第4个分量为0的列矢量。它的仿射变换为：
左（4－2－3）
　　可见，矢量V被变换成为另外一个矢量：它的齐次坐标的第4个分量也是0。
（4―2―1）
，

，
。

（4―2―2）
。

（4―2―3）
。

三维几何变换

利用齐次坐标和仿射变换，可以实现所有的三维几何变换。任何复杂的几何变换都可以分解成为比例、剪切、反射、旋转和平移等等简单变换的组合。 4.3.1 比例     在作比例和旋转变换时，都应当指定一个参考点。在此，我们先假定参考点是原点，在4.3.6节中我们将介绍绕任意点的平移和旋转变换。

比例变换是对物体按某种比例进行放大或缩小的一种几何变换。以坐标原点为参考点,沿x、y和z坐标轴分别独立地缩放α_x 、α_y 和α_z 倍的比例变换可以用齐次坐标表示如下（见图4.3）：
P′＝SP
其中，P和P′分别是用齐次坐标表示的变换前和变换后的点，P＝[x y z 1]^T, P′＝[x′ y′ z′ 1]^T; S是比例变换矩阵，
（4－3－1）
。
　图4.3 比例变换

其逆变换的变换矩阵
（4－3－2）
。
    对于任何一个三维几何变换，一旦知道了它的变换矩阵（如S），这个变换就唯一确定了。所以，下面我们重点介绍其它几何变换的变换矩阵。

posted @ 2009-09-24 17:52 王书奎(网名:无忌) 阅读(305) | 评论(0) | 编辑

 

 

Silverlight计算机图形学2 二维坐标和显示基础

图形变换一般是指将物体的几何信息经过放大、缩小、平移和旋转等几何变换后产生新的图形。它总是与相关的坐标系紧密相连的。从相对运动的观点来看，图形变换既可以看作是图形相对于坐标系的变动，即：坐标系固定不动，物体的图形在坐标系中的坐标值发生变化；也可以看作是图形不动，但是坐标系相对于图形发生了变动，从而使得物体在新的坐标系下具有新的坐标值。通常图形变换只改变物体的几何形状和大小，但是不改变其拓扑结构。
    为了在计算机屏幕或绘图仪上输出图形, 通常必须在一个图形中指定要显示的部分或全部以及显示设备的输出位置。可以在计算机屏幕上仅显示一个区域，也可以显示几个区域，此时它们分别放在不同的显示位置。在显示或输出图形的过程中，可以对图形进行平移、旋转和缩放等几何操作。如果图形超出了显示区域所指定的范围，还必须对图形进行裁剪。
本章主要内容包括:

观察流程简介; 二维几何变换 窗口到视区的变换 二维裁剪算法

有关三维的图形的变换和观察流程等内容，我们将在后面的章节中介绍。
3.1 观察流程
    在计算机图形学中，为了便于几何造型和图形的观察与显示，引入了一系列的坐标系：
a 世界坐标系：
    通常世界坐标系是一个三维笛卡儿坐标系。它是一个全局坐标系统，一般为右手坐标系。该坐标系主要用于图形场景中的所有图形对象的空间定位、观察者（视点）的位置和视线的定义等等。计算机图形系统中所涉及的其它坐标系基本上都是参照它进行定义的。

b 局部坐标系：
    为了几何造型和观察物体方便起见，独立于世界坐标系定义的二维或三维笛卡儿坐标系称为局部坐标系。在局部坐标系中定义的"局部"物体，通过指定局部坐标系在世界坐标系中的方位，利用几何变换，就可以将"局部"定义的物体变换到世界坐标系内，使之升级成为世界坐标系中的物体。

c 观察坐标系：
    观察坐标系通常是以视点的位置为原点，通过用户指定的一个向上的观察向量来定义的一个坐标系，缺省为左手坐标系。观察坐标系主要用于从观察者的角度对整个世界坐标系内的图形对象进行观察，以便简化几何物体在视平面（又成为成像面或投影面）的成像的数学演算。

d 视平面（成像面）坐标系：

    它是一个二维直角坐标系统，主要用于计算物体在成像面上的投影。一般是通过指定视方向和视点到成像面之间的距离来定义成像面（投影面）。可进一步在投影面上定义一个称之为窗口的矩形区域来实现部分成像。

e 屏幕坐标系：

    屏幕坐标系也称为设备坐标系，它主要用于某一特定的计算机图形显示设备(如光栅显示器)的表面的点的定义。在多数情况下，对于每一个具体的显示设备，都有一个单独的设备坐标系。
    在定义了成像窗口的情况下，可进一步在屏幕坐标系统中定义称为视区的有界区域，视区中的成像即为实际所观察到的图形对象。换句话说，在世界坐标系中要显示的区域称为窗口，而显示器上相应的图形输出区域称为视区（或视口）。将世界坐标系中的一部分区域中的场景映射到设备坐标系的过程称为观察变换；将二维观察变换简单地称为窗口到视区的变换，简称为窗视变换。它可以分为以下几个步骤（见图3.1）:

在场景建模的过程中，常常需要定义局部坐标系（或建模坐标系），或对物体进行平移、旋转和缩放等等几何变换。为了方便设置窗口的大小和方向，我们可以在世界坐标系中定义一个二维的观察坐标系，在观察坐标系中定义一个窗口（见图3.2）。
图3.2 世界坐标系xwoyw和观察坐标系xvoyv

图3.3 规范化的设备坐标系
　　另外，我们在规范化的坐标系（取值范围为0到1）下定义视区，如图3.3所示。可以定义多个视区。如果只定义了一个视区，则这个视区充满整个单位正方形。通过二维裁剪和窗视变换，把窗口中的场景映射到视区中。规范化的坐标系能够保证观察和变换独立于输出设备。一旦场景变换到规范化的坐标系之后，就可以通过简单的映射把各个视区中的图形输出到具体设备的绘图区。

比例变换
    比例变换是使图形按在x和y坐标轴方向分别按比例因子S_x和S_y放大或缩小的变换。它可以改变图形的大小和形状。
设平面上的一个点P的坐标为（x, y,），经过比例变换后的坐标是（x′, y′），如图3.3所示，其计算公式为：

x′＝x·Sx y′＝y·Sy

其中，Sx和Sy为比例因子。上式可以用矩阵的形式表示为：
(3-2-1)

。



不同坐标系的坐标转换


窗口到视区的坐标变换

    实际的窗口与视区的大小往往是不一样的(如图3.7和3.8所示)，为了在视区内正确地显示几何形体，必须将其从窗口变换到视区。
图3.7 窗口

图3.8 视区

设(x_w,y_w)是窗口中的任意一点，(x_v,y_v)是视区中对应的一点。则有如下关系：

,

。

化简得：
(3-3-1)

其中:

，

，

，

。

(3-3-1)式可以用矩阵表示为

裁剪

 裁剪
    在计算机图形显示的过程中,往往需要确定图形的哪些部分(包括点、线段、文字、多边形等)落在显示区域(即:视口或视区)之内，哪些部分落在显示区域之外，以便只显示位于显示区域内的那部分图形。裁剪的实质就是决定图形中哪些部分位于指定的区域内。这需要进行几何处理,以便去除落在指定区域之外的部分,保留位于指定区域以内的部分。这个过程称为裁剪。最直观的裁剪方法是把各种几何图素通过扫描转换等技术离散成为点的集合，再逐点判断其是否位于指定的区域内。那样虽然简单，但是效率太低，一般不可取。
3 线段的裁剪
    对于一条给定的线段，其裁剪过程一般包括以下几个部分：首先测试和判断它是否完全落在裁剪区之内？如果不是，再判断它是否完全落在裁剪区之外？然后,对于既不能确定完全落在裁剪区之内又不能确定完全落在裁剪区之外的线段,要计算它与一个或多个裁剪边界的交点。最后，对线段的端点进行测试，对于两个端点都落在裁剪区域内的线段就存储起来，否则就予以去除，即裁剪之。

对于端点为(x₁, y₁)和(x₂, y₂)的线段，可以用参数方程表示：

    

    当线段的某一个或两个端点都位于裁剪区域之外时，通过该线段与裁剪边界求交，可以得到参数t的值。如果交点的t值不在0和1之间，则该线段不在该裁剪边界进入裁剪区域；否则，该线段就穿入或穿过了裁剪区域。通过去除裁剪区域以外的部分，可以实现线段的裁剪。为了减少求交计算、提高选择和识别内部或外部线段的效率，设计有效的裁剪算法是非常重要的。


下面是我在网上找的文章，帮助理解，看不懂就

算，计算机图形学感觉有点难，

还好我高等数学，线性代数，概率，大学物理学得好，不然真是一点

都不懂了。

三维坐标系
理解计算机3D图形学中的坐标系变换

     要谈坐标系变换，那么坐标系有哪些呢？依次有:物体坐标系，世界坐标系，相机坐标系，投影坐标系以及屏幕坐标系.我要讨论的就是这些坐标系间的转换。
     这些坐标系不是凭空而来，他们都是为了完成计算机3D图形学最最最基本的目标而出现.
      计算机3D图形学最最最基本的目标就是:将构建好的3D物体显示在2D屏幕坐标上.
      初看好像就是将最初的物体坐标系转换到屏幕坐标系就可以了呀，为什么多出了世界坐标系,相机坐标系，投影坐标 系。这是因为:在一个大世界里有多个物体，而每个物体都有自己的坐标系，如何表述这些物体间相对的关系，这个多出了世界坐标系；如果只需要看到这个世界其 中一部分，这里就多出了相机坐标系；至于投影坐标系那是因为直接将3D坐标转换为屏幕坐标是非常复杂的(因为它们不仅维度不同,度量不同（屏幕坐标一般都 是像素为单位,3D空间中我们可以现实世界的米，厘米为单位），XY的方向也不同，在2D空间时还要进行坐标系变换),所以先将3D坐标降维到2D坐标, 然后2D坐标转换到屏幕坐标。
理解3D图形学的第一步:理解左手坐标系与右手坐标系
      为什么会有左手坐标系与右手坐标系之分？
      在3D空间(没错！就是3D)中，所有2D坐标系是等价的（就是通过一系列的仿射变换，可以互相转换）
      而3D坐标系不是等价的，通过仿射变换，是无法将左手坐标系转换到右手坐标系；也就是说，物体坐标系用的就是左手坐标系，世界坐标系用的是右手 坐标系，那么物体可能就是不会是我们所希望的样子了，可能是倒立的，也可能是背对着我们的，所以我们要区分左手坐标系与右手坐标系。也许在4D空间，左右 手坐标系就可以互相变换了吧。
      进入正题吧:
     首先讨论的是物体坐标系->世界坐标系
      前面说了为了描述多个物体间相对的关系，这里引进了世界坐标系,所以世界坐标系是个参考坐标系。
      这一步的目的将所有的物体的点都转移到世界坐标系，这里主要涉及的是旋转，缩放，平移等。
      不过我将详细说明为何及如何用矩阵来描述这些变换。
      例:如果有两个坐标系C与C`, C`是C绕Z轴旋转θ得到的。下面是各坐标轴的变换：
             
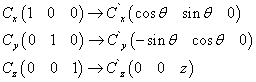
     如果是C坐标系的点P（x, y, z），而在C`的表示就是
   
     这时该如何建立矩阵呢? 答案就是区分你用的是行向量还是列向量.也许有人会问为什么不区分是左手坐标系还是右手坐标系呢？因为C可以变换到C`,那么他们一定是同在左手坐标系或右手坐标系,变换只能在可以互相转换的坐标系之间进行。
      如果你用的是行向量：由于行向量只能左乘矩阵(注意乘与乘以的区别)
      所以矩阵形式应该是这样
    
     只有这样，在左乘矩阵时才能得到上面P`的形式。
    
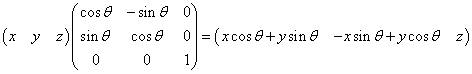
     如果你用的是列向量: 由于列向量只能右乘矩阵(注意乘与乘以的区别)
     所以矩阵形式应该是这样
    
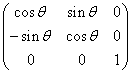
     只有这样，在右乘矩阵时才能得到上面P`的形式。
  
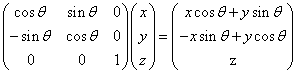
     至于如何旋转，缩放，平移我不在多说。
     …………………………………觉得自己好像跑题了.还好这两个坐标系变换很简单。
     我们再讨论世界坐标系->相机坐标系
     引进相机的目的就是只需看到世界的一部分，而哪些是可以在相机里看到的，就需要进行筛选。将物体转换到相机坐标系，这样相机坐标系进行筛选时就会简单很多。这里的重点是构建相机坐标系。
     物体坐标系，世界坐标系是美工在绘制时就定义好了的。而相机坐标系是需要程序实时构建的。（当然这是通常情况下，如果你要建立一个世界，这个世界都是围绕 你转，要实时改变所有物体坐标系，固定相机坐标系（其实这时候相机坐标系就是世界坐标系），建立一个地心说的世界，我也没办法，你的思维也太不一样了。）
     如何构建相机坐标系呢？首先我们要明确目标：我们是要构建3D坐标系(好像是废话)，三个坐标轴要互相垂直(也好像是废话).
      我们一般用UVN相机。例如:D3D的D3DXMatrixLookAtLH，D3DXMatrixLookAtRH，OGL的gluLookAt(右手坐标系).
      如何建立呢UVN相机呢? 我们就要利用叉积这个工具了：两个不平行，不重叠的向量的叉积可以得到与这两个向量互相垂直的向量。
      如果有了相机的位置与目标的位置那么我们可以确定一个Z轴（有人问为什么是Z轴，因为物体的远与近我们就习惯用Z值来表示的）。求Z轴时要注意 是左手坐标系还是右手坐标系，左右手坐标系XY轴方向相同时，Z轴的方向相反。所以左手坐标系是目标位置减去相机位置，而右手坐标系则是相机位置减去目标 位置。记得normalize
     这是我们要得到X与Y轴了。如何求X，Y轴呢？
     一般方法是：
     1、选择一个临时Y轴，
     2、对临时Y 与Z 轴进行叉积求得一个X轴
     3、X轴再与Z轴进行叉积，得到一个Y轴。
     有了XYZ就可以求出旋转的相机矩阵了。
     如何选择一个Y轴呢？大多数情况下是（0，1，0），但是如果是相机位置E与目标位置T垂直,即（E-T=（0，+/-1，0）时），这时就不能用(0,1,0)了， 因为两个平行向量的叉积是零向量，所以我们就要另选一个Y轴。
     但是我觉得我们可以改变方法。
      如果不能选Y轴，我们就选择一个临时X轴，这个临时Ｘ轴就是（1，0，0）。
     然后再对临时X轴与Z轴进行叉积求得一个Y轴。
     最后Y轴再与Z轴进行叉积，得到X轴。
      这样可以得到XYZ轴。
      最后再根据行向量与列向量建立相机矩阵，再进行平移。

     相机坐标系->投影坐标系.
     投影的目的就是：降维.
      两种投影方式：正交投影与透视投影.
      在我们TEAM中易颖已经写了，我就不多说了，大家去看他的文章。

     投影坐标系->屏幕坐标系
      这是最简单的。2D坐标变换。也不多说。

转载文章2：http://www.xingousi.com/computer/computergraphics.htm

计算机图形学笔记(Part 1 )：计算机图形学透视投影变换原理及一点和两点透视

 

一、平行互分法

吴英凡所写的《透视作图的新方法——交点法体系》，其中谈到的平行互分法，还是有道理的。

其实简单点说，就是透视图上的两条“原来空间中的平行线”（在画面上透视投影为相交于灭点），通过其中一条透视投影直线的端点画另一条透视投影直线的平行线，必平行于画面；这第三条线在画面的透视投影的灭点必然在另一条透视投影线上。

 

 

 

二、透视投影变换学习总结

1、用多维数列表示低维空间坐标,加深理解齐次坐标表示法。

    齐次坐标表示法可以方便地运算，同时形状不变。[x,y,z,0]表示一个无穷的点。

   

2、透视投影变换公式可以看成两个矩阵的乘积，其中一个做透视变换，另外一个作正投影

   保留的z'值的确切含义：指的是在完全作完透视投影变换之前，仅作透视投影之后的一条线.

   它的几何意义见李建平《计算机图形学原理教程》第44页。

3、左手和右手坐标系的坐标转换

   “视点坐标系与一般的物体所在的世界坐标系不同，它遵循左手法则，即左手大拇指指向Z正轴，与之垂直的四个手指指向X正轴，四指弯曲90度的方向是Y正轴。而世界坐标系遵循右手法则的。”

4、视点坐标系的透视变换公式很重要！！王飞著计算机图形学书65页

5、z'值的确切含义：指的是在完全作完透视投影变换之前，仅作透视投影之后的一条线

 

 

 

三、两点透视的变换矩阵：

王飞编著《计算机图形学基础》的道理是：

从平面图形的平移、旋转、错切开始推导，两点透视的变换矩阵可以看成是：

物体本身有一个物体坐标系——xw,yw,zw，视点作为原点又构成一个视点坐标系——xe，ye，ze，物体坐标系z轴朝上，y轴朝向远处；而视点坐标系y轴朝上，z轴朝向远处。

这样，最终的二点透视状态可以这样取得，首先把物体的位置的物体坐标系表示法转化为视点坐标系的表示法（第一个矩阵），然后围绕视点坐标系的y轴旋转（第二个矩阵），然后在x，y，z方向上平移（第三个矩阵），最后做透视变换（第四个矩阵），它的原文是把平移放在第二步，我在平移之前转动，目的是保证了物体旋转的轴在离它不远的地方：

我使用的矩阵变换如下，原文是是把平移放在第二步：

[xw,yw,zw,1]* ***

 

最后所得结果是一个新的矩阵，

[xe ye ze 1]=[cos*xw-sin*yw+l   zw+m   2sin*xw+2cos*yw+2n-d   (sin*xw+cos*yw+n）/d]

把最后一项变成1，可得

=[(cos*xw-sin*yw+l)*d/(sin*xw+cos*yw+n   (zw+m)*d/(sin*xw+cos*yw+n)   （2sin*xw+2cos*yw+2n-d）*d/(sin*xw+cos*yw+n)    1 ]

即：

Xe= (cos*xw-sin*yw+l)*d/(sin*xw+cos*yw+n)

Ye=(zw+m)*d/(sin*xw+cos*yw+n)

Ze=(2sin*xw+2cos*yw+2*n-d)*d/(sin*xw+cos*yw+n)

 

实际上我的delphi程序里面是这样的：

xe:=trunc((cos(angle)*eee[ii][k].X-sin(angle)*eee[ii][k].Y+l)*d/(sin(angle)*eee[ii][k].X+cos(angle)*eee[ii][k].Y+n));

        ye:=trunc((hhh[ii][k]+m)*d/(sin(angle)*eee[ii][k].X+cos(angle)*eee[ii][k].Y+n)); //透视变换

        //ze可以考虑使用作为消隐

Ze:=trunc((2*sin(angle)*xw+2*cos(angle)*yw+2*n-d)*d/(sin(angle)*xw+cos(angle)*yw+n));

 

 

四、通过变换过的两点透视的结果xe,ye，zw和*，反求原来的物体坐标xw,yw

即：xe,ye，zw和已知，求出xw,yw

根据：

Xe= (cos*xw-sin*yw+l)*d/(sin*xw+cos*yw+n)          （1）

Ye=(zw+m)*d/(sin*xw+cos*yw+n)                         （2）

Ze=（2sin*xw+2cos*yw+2n-d）*d/(sin*xw+cos*yw+n) （3）

（1）除以（2）得

Xe/Ye= (cos*xw-sin*yw+l)/ (zw+m)

(Xe*(zw+m))/Ye=cos*xw-sin*yw+l

(Xe*(zw+m))/(Ye* cos)=xw-tan*yw+l/cos

Xw=(Xe*(zw+m))/ (Ye* cos) - (ye*l)/(Ye* cos)+( sin*yw*ye)/ (Ye* cos)

 

Xw=(Xe*(zw+m)+ sin*yw*ye- ye*l)/ (Ye* cos)            (4)

 

由（2）得

Ye*(sin*xw+cos*yw+n)= (zw+m)*d

Ye*(sin*xw)+ye* cos*yw+n*ye=(zw+m)*d

把（4）代入上式得

Ye* sin*(Xe*(zw+m)+ sin*yw*ye- ye*l)/ (Ye* cos)+ye* cos*yw+n*ye=(zw+m)*d

约去ye，得

sin*(Xe*(zw+m)+ sin*yw*ye- ye*l)/ cos+ye* cos*yw+n*ye=(zw+m)*d

tan*(Xe*zw+xe*m+ sin*yw*ye- ye*l) +ye* cos*yw+n*ye=(zw+m)*d

tan*Xe*zw+xe*m *tan- ye*l*tan+ sin*tan*yw*ye+ye* cos*yw+n*ye=(zw+m)*d

(sin*tan*ye+ye* cos)*yw+ tan*Xe*zw+xe*m *tan- ye*l*tan+n*ye=(zw+m)*d

 

最后得

Yw=[(zw+m)*d- tan*Xe*zw- xe*m *tan+ ye*l*tan- n*ye]/ (sin*tan*ye+ye* cos) （5）

而前面已经得到

Xw=(Xe*(zw+m)+ sin*yw*ye- ye*l)/ (Ye* cos)            (4)

 

实际上相当于opengl里面的逆变换，从鼠标选中的屏幕位置来确定对应的三维空间中位置，opengl使用gluUnProject和gluUnProject4来计算。